Критосистема RSA

Для шифрования выбирают целое число N = p q, где p и q – два больших простых числа. Сообщение M представляется одним из чисел

M Î {1, 2, ¼, N –1}.

Формулы, описывающие шифрование/дешифрование, имеют следующий вид:

, ,

где K – открытый ключ шифрования, k – секретый ключ дешифрования.

Покажем, что возведение в степень

E^k =(M^K) ^k = M^Kk mod N,

выполняемое при дешифровании, действительно восстанавливает сообщение M.

В RSA пара ключей формируется по правилу

kK = 1 mod j(N), (*)

что эквивалентно

kK = 1 + l j(N),

где l – целое число, а j(N) – функция Эйлера, которая определяет число целых чисел меньших N и взаимно простых с ним.

По теореме Эйлера, если M и N – взаимно простые числа,

M ^{j (N)} = 1 mod N.

Отсюда

M ^kK = M ^{1+ l j (N)} = M (M ^{j (N)}) ^l = M ×1 ^l = M mod N, (**)

т.е. происходит дешифрование сообщения.

В то же время можно доказать, что специальный выбор модуля N в виде произведения N = pq двух простых чисел p и q обеспечивает выполнение равенства (**), т.е. дешифрование, вообще при любых M, не обязательно взаимно простых с N. Отметим также, что степень M ^K не должна быть меньше N. При невыполнении данного условия криптограмма принимает вид

,

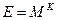и легко вскрывается без вычислений по модулю, т.к. открытый ключ K известен.

Рассмотренные соотношения указывают путь формирования ключей. Вначале выбирают очень большие случайные простые числа p и q, отличающиеся друг от друга на несколько десятичных разрядов, так чтобы произведение N = pq имело длину не менее 768 бит (по данным 2001 года). Вычисляют функцию Эйлера

j(N) = (p – 1)(q – 1).

Из равенства (*)

K k = 1 mod j(N),

откуда следует, что оба ключа взаимно обратные числа по модулю j(N).

Открытый ключ K выбирают среди чисел меньших и взаимно простых с j(N). Закрытый ключ k вычисляют

k = K ^{– 1} mod j(N)

с помощью алгоритма Евклида, что не является сложной задачей. Завершив подготовительные операции, открытый ключ K и модуль N помещают в открытый справочник, приняв меры, гарантирующие невозможность подмены. Числа k, p и q хранят в секрете.

Таким образом, оба ключа RSA задаются парами целых чисел: (K, N) и (k, N), причем числа K и k равноправны, т.е. ключи можно поменять местами, и использовать k как открытый ключ шифрования, а K как закрытый ключ дешифрования

Когда авторы R. Rivest, A. Shamir, L. Adleman (Ривест, Шамир, Адлеман) в 1977 году предложили криптосистему RSA, они зашифровали фразу “Its all Greek to me”, представленную в цифровой форме M. Были опубликованы значения E, K, N с указанием, что 129 десятичных разрядов N получены при умножении 64- и 65-разрядных чисел p и q. Факторизация N и вскрытие криптограммы были выполнены примерно за 220 дней лишь в 1994 году после предварительной теоретической подготовки. В работе принимало участие 600 добровольцев и 1600 компьютеров, объединенных в сеть с помощью Интернет.

Дата добавления: 2015-10-26