Метод аналитической аппроксимации

Метод основан на аппроксимации характеристики нелинейного элемента аналитической функцией, которая должна, с одной стороны, достаточно точно отображать исходную нелинейную характеристику на участке перемещения рабочей точки, а с другой стороны, обеспечивать возможность достаточно несложного интегрирования полученного дифференциального уравнения (в частности, с использованием табличных интегралов).

Метод применим к нелинейным цепям с одним накопителем энергии, описываемым дифференциальными уравнениями первого порядка, а также к цепям, описываемым уравнениями, сводящимися к уравнениям первого порядка путем замены переменных.

Ценность метода заключается в получении выражения исследуемой величины в общем виде, что позволяет осуществлять требуемый анализ процессов при варьировании параметров схемы.

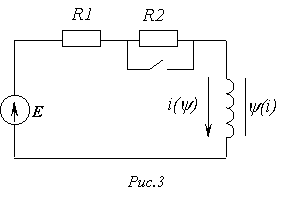
В качестве примера использования метода определим ток в схеме на рис. 3, полагая, что характеристика нелинейной катушки имеет вид типовой кривой на рис. 2.

1. Для решения задачи выберем выражение аналитической аппроксимации вида 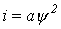. Определяя параметр 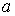из условия соответствия данной функции точке установившегося послекоммутационного режима, получим

,

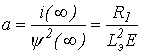(4)

где .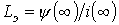

2. Подставив в уравнение переходного процесса

аналитическое выражение тока с учетом (4), получим

(5)

Разделяя переменные и решая (5) относительно времени, запишем

(6)

где 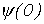– начальное значение потокосцепления, соответствующее значению тока в момент коммутации .

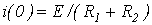Выражение (6) соответствует табличному интегралу; в результате получаем

.

(7)

Подставив в последнее соотношение выражение потокосцепления в виде

,

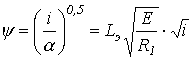перепишем (7) как

.

Метод кусочно–линейной аппроксимации

Данный метод основан на замене характеристики нелинейного элемента отрезками прямых, на основании чего осуществляется переход от нелинейного дифференциального уравнения к нескольким (по числу прямолинейных отрезков) линейным, которые отличаются друг от друга только значениями входящих в них коэффициентов. Необходимо помнить, что каждое из линейных уравнений справедливо для того временного интервала, в течение которого рабочая точка перемещается по соответствующему линеаризованному участку. Временные границы для каждого участка определяются исходя из достижения одной (любой) из переменных, определяющих характеристику нелинейного элемента, своих граничных значений для рассматриваемого прямолинейного участка. В соответствии с законами коммутации значения тока в ветви с катушкой индуктивности или напряжения на конденсаторе в эти моменты времени являются начальными значениями соответствующих переменных для соседних прямолинейных участков, на основании чего определяются постоянные интегрирования. Значение параметра линеаризуемого нелинейного элемента для каждого участка ломаной определяется тангенсом угла, образованного рассматриваемым прямолинейным отрезком с соответствующей осью системы координат.

В качестве примера рассмотрим применение данного метода для решения предыдущей задачи.

1. Заменим рабочий участок зависимости (см. рис. 2) двумя прямолинейными отрезкам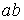и и . Первому из них соответствует уравнение 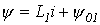, второму – 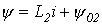. При этом начальная точка 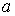определяется током , а конечная точка - током .

Соответствующие этим участкам индуктивности

;

.

2. В соответствии с указанной линеаризацией нелинейное дифференциальное уравнение состояния цепи

заменяется двумя линейными:

;

.

3. Решением первого уравнения является

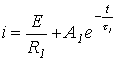
и второго -

,

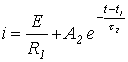где ; ; ; .

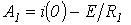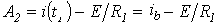Время t1, соответствующее моменту перехода с первого участка на второй, определим из уравнения

,

откуда

.

Дата добавления: 2015-10-26