
Читайте также:
|
Принцип компенсации основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви.
Для доказательства теоремы выделим из схемы произвольную ветвь с сопротивлением 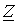 , по которой протекает ток
, по которой протекает ток  , а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А (см. рис. 6,а).
, а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А (см. рис. 6,а).
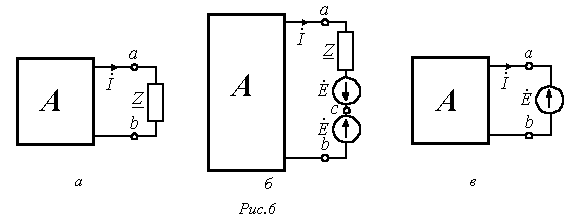
При включении в ветвь с 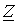 двух одинаковых и действующих навстречу друг другу источников ЭДС с
двух одинаковых и действующих навстречу друг другу источников ЭДС с  (рис. 6,б) режим работы цепи не изменится. Для этой цепи
(рис. 6,б) режим работы цепи не изменится. Для этой цепи
 . .
| (12) |
Равенство (12) позволяет гальванически соединить точки а и c, то есть перейти к цепи на рис. 6,в. Таким образом, теорема доказана.
В заключение следует отметить, что аналогично для упрощения расчетов любую ветвь с известным током  можно заменить источником тока
можно заменить источником тока  .
.
7.
| Замена нескольких параллельных ветвей, содержащих источники ЭДС и источники тока, одной эквивалентной |
При расчете сложных схем существенное облегчение дает замена нескольких параллельно включенных ветвей, содержащих источники ЭДС, источники тока и резисторы, одной эквивалентной.
Необходимо, чтобы при любых значениях тока I, притекающего к выделенному участку из остальной части схемы, напряжение Uab в обеих схемах было бы одинаковым (рис. 1.10).
 Рис. 1.10. Исходная (а) и эквивалентная (б) схемы источников
Согласно I закону Кирхгофа ток во внешней цепи
Рис. 1.10. Исходная (а) и эквивалентная (б) схемы источников
Согласно I закону Кирхгофа ток во внешней цепи
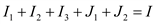
 (1.9) (1.9)
 , (1.10)
где m – число ветвей с источниками ЭДС; n – число ветвей с источниками тока.
Для схемы на рис.1.10б , (1.10)
где m – число ветвей с источниками ЭДС; n – число ветвей с источниками тока.
Для схемы на рис.1.10б
 .
Равенство токов в обеих схемах возможно, если .
Равенство токов в обеих схемах возможно, если
 (1.11)
Если направление ЭДС или источника тока изменить на обратное, то они войдут в формулу (1.11) со знаком «–». Если ЭДС в какой-либо ветви нет, то соответствующее слагаемое в числителе (1.11) будет отсутствовать, но проводимость этой ветви в знаменателе формулы останется. (1.11)
Если направление ЭДС или источника тока изменить на обратное, то они войдут в формулу (1.11) со знаком «–». Если ЭДС в какой-либо ветви нет, то соответствующее слагаемое в числителе (1.11) будет отсутствовать, но проводимость этой ветви в знаменателе формулы останется.
|
Дата добавления: 2015-10-26; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод наложения | | | Метод узловых потенциалов |