Определение по карте расстояний и координат точек

4.1 Определение расстояний

Любой из трёх видов масштабов – численный, именованный или графический можно использовать для определения расстояний на местности с помощью карты. Решают и обратную задачу, в которой определяют расстояние на карте по заданному расстоянию на местности.

Пусть измеренный линейкой отрезок на карте масштаба 1:5000 равен 49,4 мм. Умножив его на знаменатель масштаба, получим 49,4´5000=247000 мм=247 м.

Используя именованный масштаб "в 1 см 50 м", переведём расстояние на карте в сантиметры (4,94), умножим его на 50 м и получим 247 м.

При использовании графического масштаба искомое расстояние на карте фиксируют циркулем-измерителем. Затем, если расстояние определяют по линейному масштабу (рисунок 4.1), правую ножку циркуля-измерителя устанавливают на тот штрих первой шкалы, чтобы левая ножка оказалась в диапазоне второй шкалы. Искомое расстояние на местности равно сумме отсчётов по двум шкалам.

При использовании поперечного масштаба (рисунок 4.2) зафиксированный циркулем-измерителем отрезок перемещают по вертикали до тех пор, пока левая ножка не будет наилучшим образом совмещаться с какой- либо трансверсалью. При этом обе ножки должны находится на одной и той же горизонтальной линии, а правая ножка – на каком либо штрихе первой шкалы. Искомое расстояние на местности равно сумме отсчётов по трём шкалам масштаба.

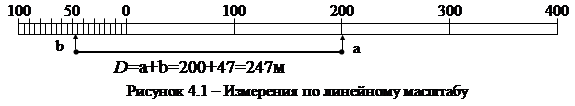
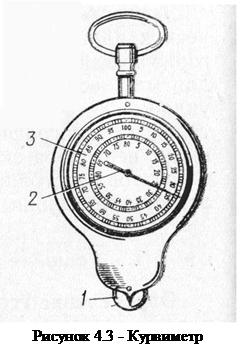При определении криволинейных расстояний удобно использовать курвиметр (рисунок 4.3). Путь, пройденный колесом 1, фиксируется стрелкой 2 по циферблату 3.

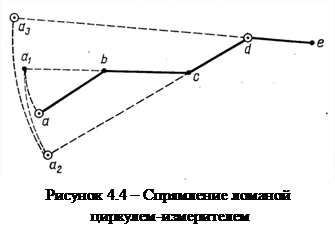
Спрямить криволинейный отрезок можно циркулем-измерителем, наращивая его раствор – расстояние между иголками ножек небольшими отрезками кривой, которые можно считать прямолинейными. Для этого вначале циркулем-измерителем фиксируют отрезок ab (рисунок 4.4). Затем последовательно иголки ножек переставляют: левую - в точку а₁, правую - в точку с, левую - в точку а₂, правую - в точку d, левую - в точку а₃, правую - в точку е. В результате раствором циркуля-измерителя будет зафиксирован спрямлённый отрезок а₃е.

Задание 2.

1. Нарисовать линейный и поперечный масштабы с основанием 20 мм для численного масштаба, указанного в таблице 4.1.

2. Вычислить точность масштаба.

3. Определить по обоим масштабам расстояние на местности D по длине d отрезка на карте.

,

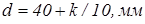где k – две последние цифры кода студента.

4. Вычертить извилистую линию длиной 5¸8 см. Определить её длину на местности с помощью циркуля-измерителя и (или) курвиметра для заданного масштаба.

Таблица 4.1 – Исходные данные

Последняя цифра кода студента, k0	Масштаб	Высота сечения рельефа, м
	1:200	0,2
	1:500	0,25
	1:1000	0,5
	1:2000
	1:5000
	1:10000	2,5
	1:25000
	1:50000
	1:100000
	1:200000

4.2 Определение прямоугольных координат

Для определения координат точек на карте или нанесения точек по координатам используется координатная сетка, линии которой подписаны по всем 4-м рамкам карты. Чтобы найти координаты точки А (рисунок 4.5) вначале записывают абсциссу x нижней стороны квадрата, в которой находится точка. Она равна 6066 км. Затем измеряют расстояние dx от этой стороны квадрата до точки А и определяют это расстояние на местности любым из рассмотренных в п 4.1 способом. Оно равно 560 м. Следовательно, абсцисса составит x = 6066000+560=6066560 м.

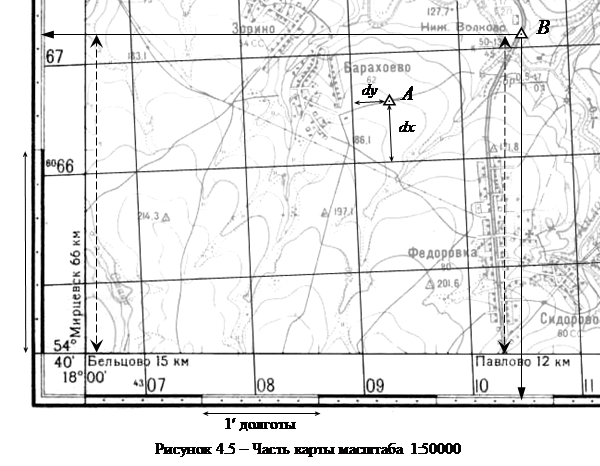При определении ординаты y записывают её для левой стороны квадрата (4309 км), измеряют расстояние dy от этой стороны до точки А, находят расстояние на местности (325 м), складывают обе величины и получают y = 4309000+325=4309325 м.

4.3 Определение географических координат

Географические координаты – широта и долгота показаны на всех четырёх рамках карты. Для этого используется специальная разграфка минут по широте и долготе (рисунок 4.5), нанесённая за внутренней рамкой листа карты.

Каждая минута разделена точками на 6 частей, поэтому интервал между ними составляет 10². Значения координат подписаны только в углах карты. Так в нижнем левом углу подписана широта южной (нижней) рамки 54°40¢ и долгота западной (левой) рамки 18°00¢. Однако линий равных широт и долгот (параллелей и меридианов), подобных координатной сетке, на карте нет.

Для определения географических координат нужно спроецировать точку на ближайшие рамки широты и долготы по линиям, параллельным рамкам карты. Эти линии, в общем случае, не параллельны линиям координатной сетки из-за сближения меридианов. Затем отсчитывают координаты по шкалам широт и долгот. При отсчитывании по шкале широт к координате нижней рамки прибавляют число минут, десятки секунд и единицы секунд (интерполированием на глаз) от нижней рамки до проекции точки. Для долготы поступают аналогично. Так для точки В (рисунок 4.5) будем иметь широту j =54°40¢+1¢34²=54°41¢34² и долготу l =18°00¢+3¢43²=18°03¢43².

При проецировании точки на шкалы географических координат линии, параллельные рамкам карты, рисовать не нужно. Поступают обычно так. При определении широты циркулем-измерителем или на листе бумаги фиксируют отрезок dj от точки В до южной или северной внутренней рамки (рисунок 4.5). Затем этот отрезок откладывают по шкале широты, совместив один конец отрезка с этой же линией рамки, а по другому концу отрезка отсчитывают широту. При определении долготы целесообразно проецировать точку подобным способом на ближайшую шкалу долготы – северную или южную, потому что меридианы на карте не параллельны между собой: чем ближе точка к шкале долготы, тем меньше ошибка.

Более точно определение координат можно выполнить с помощью длинной линейки. Линейку вращают вокруг искомой точки до тех пор, пока отсчёты по двум противоположным шкалам широты или долготы не станут одинаковыми. Они и являются окончательными.

Задание 3. Определить прямоугольные и географические координаты двух точек на рисунках 4.6 (для нечётной предпоследней цифры) или 4.7 (для чётной предпоследней цифры). Номер первой точки равен предпоследней цифре кода студента, умноженной на 10 (например, для предпоследней цифры 3 номер точки 30). Номер второй точки равен последней цифре кода студента.

4.4 Определение высот

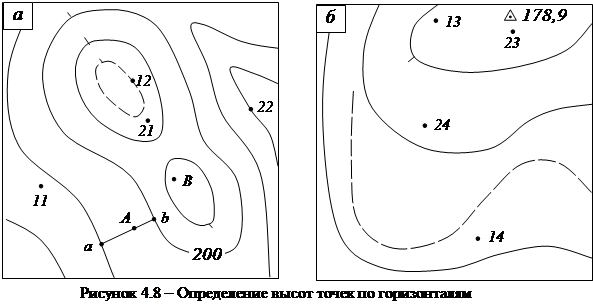
На карте рельеф показывают горизонталями. Если точка находится на горизонтали, то высота (отметка) точки равна высоте данной горизонтали. Для определения высоты H_A точки А, лежащей между горизонталями (рисунок 4.8, а), определяют высоты младшей H_a и старшей H_b горизонталей.

При этом их разность равна высоте сечения рельефа:

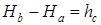. (4.1)

Затем измеряют линейкой по линии, проходящей через точку А и пересекающей обе горизонтали на минимальном расстоянии, два отрезка aA; ab и вычисляют

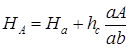. (4.2)

На рисунке имеем aA = 9,5 мм и ab = 15.5 мм. Если, например, высота сечения h_c рельефа равна 5 м, то H_a=195 м и H_b=200 м. Следовательно

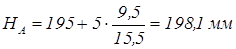
Если младшей или старшей горизонтали нет, то подобное интерполирование выполняют от имеющейся горизонтали до точки с подписанной отметкой (на рисунке б точки 13 и 23). Если нет и точки с отметкой, то высоту искомой точки (на рисунке а точка В) можно считать равной высоте ближайшей горизонтали.

Задание 4. На рисунке 4.8 определить высоты 4-х точек: 11-14- для нечётной предпоследней цифры кода студента и 21-24 - для чётной предпоследней цифры. Высоту сечения рельефа на рисунках выбрать из таблицы 4.1. Оба рисунка перерисовать (приблизительно, не копируя) и подписать высоты всех горизонталей.

Дата добавления: 2015-10-26