Условная вероятность. Независимость событий. Теоремы умножения вероятностей зависимых и независимых событий.

Понятие случайного события. Элементарное, сложное, невозможное, достоверное события. Операции над событиями (равенство, объединение, пересечение, отрицание, разность). Примеры.

Вероятность – некоторое число в интервале [0;1].

Совокупность всех возможных, различных, конкретных исходов испытаний называется пространством элементарных событий.

Сложным событием называется произвольное подмножество пространства элементарных событий.(wtf????)

сложным называется событие состоящие из нескольких связанных между собой событиями

нарисовать диаграммы Эйлера-Вена для всех случаев и будет счастье

Классическое определение вероятности. Примеры.

определение классической вероятности

классическая веротяность предполагает что все исходы экспиримента равновероятны

СВОЙСТВА:

Основные формулы комбинаторики. Примеры.

Пусть множество А состоит из n различных элементов различных типов, причем K₁ элементов I-ого типа, К₂ элементов II-ого, …, K_m элементов m-ого типа. Тогда всевозможные множества из n элементов называются перестановкой с повторениями.

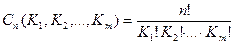
Геометрическая вероятность. Примеры.

Теоремы сложения вероятностей совместных и несовместных событий. Примеры.

если события совместны то вероятность их суммы P(A+B)= P(A) + P(B) - P(A)*P(B)
6. Противоположные события. Вероятность появления хотя бы одного события. Примеры.

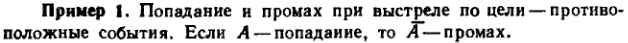
Вероятность появления хотя бы одного из событий:

Условная вероятность. Независимость событий. Теоремы умножения вероятностей зависимых и независимых событий.

Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной;

Если же налагаются и другие дополнительные условия, то вероятность события называют условной.

Условной вероятностью называют вероятность события , вычисленную в предположении, что событие е уже наступило.

Опр. Условная вероятность события при условии, что событие уже наступило, по определению, равна

Теорема. (Умножения двух событий). Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

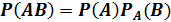
(Доказательство через определение условной вероятности).

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

Пусть вероятность события В не зависит от появления события А.

Опр. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

Итак, если событие В не зависит от события A, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.

Для независимых событий теорема умножения 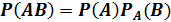имеет вид

Опр. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.

Если события независимы в совокупности, то независимы события .

---

Дата добавления: 2015-10-26