
Читайте также:
|
Криминологический прогноз с учётом данных демографии
Практикум по курсу
«Правовая статистика»
Санкт-Петербург
Введение
Цель выполнения практической работы «Криминологический прогноз с учётом данных демографии» состоит в приобретении студентами опыта решения аналитических задач из области социологии и криминологии с помощью ЭВМ. Основой для работы является практикум по электронным таблицам Excel и лекционный материал по теме «Основы теории вероятности» в объёме курса «Информатика и математика».
Для выполнения данной работы студенты получают электронный шаблон работы. Он представляет собой рабочую книгу Excel, на двух листах которой размещены готовые озаглавленные таблицы. Заполнение таблиц не представляет большого труда, особенно при применении заполнения ячеек путём копирования с помощью мыши.
Таблицы выполнены в цвете. Заполнению подлежат только белые ячейки таблиц. Области в виде серых прямоугольников отмечают места для подлежащих построению диаграмм. В некоторые белые ячейки таблиц введены числа и формулы красным цветом. Эти ячейки должны остаться в ходе работы без изменений. Высоты строк и ширины столбцов таблиц также не должны изменяться.
Выполнение работы предполагает ознакомление с изложенными в настоящем Руководстве расчётными соотношениями для моделирования, самостоятельное заполнение электронных таблиц в строгом соответствии с порядком выполнения, анализ результатов и подготовку ответов на контрольные вопросы (располагаются в конце Руководства).
В Приложении Руководства помещены распечатки листов электронного шаблона практической работы на Excel. Слова в тексте Руководства, имеющие жирное начертание без засечек, соответствуют словам, встречающимся при работе на ЭВМ (в меню, диалоговых окнах, таблицах Excel, на клавиатуре и т.п.).
Практическая работа.
КРИМИНОЛОГИЧЕСКИЙ ПРОГНОЗ
С УЧЁТОМ ДАННЫХ ДЕМОГРАФИИ
Цель работы:
изучение основ моделирования процессов на ЭВМ,
моделирование процессов возможного изменения возрастного распределения и численности населения России в течение XXI века на основе данных Госкомстата, а также
исследование их влияния на вычисляемые с их использованием показатели преступности.
РаСчётные соотношения для моделирования
1. Буквально все явления окружающего мира, не исключая и социальные, обладают изменчивостью своих свойств во времени. И их полное математическое описание является, по сути дела, описанием процессов.
Математическое описание процессов представляет собой задание функции, среди аргументов которой имеется переменная, имеющая смысл времени.
Один из способов задания такой функции – это изучение изменения числовых величин, описывающих процесс, на малых отрезках времени, а затем, на основе этого, составление уравнения, в котором последующие значения процесса выражены через предыдущие.
Моделирование процессов на ЭВМ, т.е. нахождение функций, описывающих их во времени, имеет две существенные особенности.
Первая. На ЭВМ любая функция может вычисляться только в точках, т.е. при фиксированных значениях аргумента. Применительно к моделированию процессов на ЭВМ это означает, что рассмотрение функции, описывающей процесс, на определённом отрезке времени есть вычисление её значений на конечном множестве точек, имеющих смысл последовательности отстоящих друг от друга моментов времени. Т.е. время при моделировании на ЭВМ из непрерывного превращается в дискретное. Значения процесса рассматриваются через секунду, день, год – в зависимости от решаемой задачи.
Другая особенность моделирования на ЭВМ заключается в том, что найденная функция чаще всего не имеет аналитического (формульного) представления и поэтому выражается таблично или в виде графика.
2. Рассмотрим теперь более подробно условия и порядок моделирования процессов на ЭВМ, который далее и будет применён для прогнозирования изменения во времени численности населения и уровня преступности.
Для начала моделирования процесса необходимы следующие три предпосылки.
1) Интересующее явление, процесс, в каждый момент времени t должно быть представлено в виде набора переменных, описывающих количественную сторону этого процесса:
 ,
,  , …,
, …,  , …,
, …,  . (1)
. (1)
Это могут быть: численность, стоимость, возраст, доля и т. д. – в зависимости от решаемой задачи.
2) На основании знаний из предметной области должны быть выяснены зависимости, позволяющие через значения переменных, описывающих процесс в момент времени t, т.е. через  , …,
, …,  , вычислять значения каждой из них в последующий момент
, вычислять значения каждой из них в последующий момент  , т.е. находить
, т.е. находить  , …,
, …,  . Это означает, что должны быть известны уравнения типа
. Это означает, что должны быть известны уравнения типа
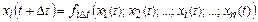 . (2)
. (2)
где  – функция временнòй связи через интервал D t для i -той переменной. (Всего n уравнений, т.к. n переменных.)
– функция временнòй связи через интервал D t для i -той переменной. (Всего n уравнений, т.к. n переменных.)
3) Должен быть установлен начальный момент времени t 0, с которого будет начато моделирование процесса, и должны быть заданы начальные значения переменных, т.е.
 ,
,  , …,
, …,  . (3)
. (3)
Теперь можно приступать к моделированию разворачивания процесса во времени.
1) Подставим начальные значения переменных, (3), во все n уравнений типа (2). Произведя вычисления, мы получим значения всех переменных процесса в следующий момент времени:
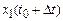 ,
,  , …,
, …,  . (3а)
. (3а)
2) Теперь получившиеся значения, (3а), снова подставим в уравнения типа (2). В результате найдём значения переменных уже в третий момент времени:
 ,
,  , …,
, …,  . (3б)
. (3б)
3) Подставив (3б) в (2), вычислим переменные для четвёртого момента времени
 ,
,  , …,
, …,  . (3в)
. (3в)
4) И так далее.
В результате такого многократного повторения будет найдена временная последовательность значений для каждой i- той переменной процесса:
 ,
,  ,
,  ,
,  ,...
,...
Это и есть искомая модель процесса во времени.
Она удобна тем, что многократные вычисления по одним и тем же формулам легко организуются с помощью ЭВМ, в чём можно будет убедиться в дальнейшем.
3. В настоящей работе моделируется процесс возможного изменения показателей преступности, вызванный изменением численности населения и его возрастного распределения на примере России на всём протяжении XXI века.
На преступность как явление влияет огромное множество различных факторов. Однако здесь для простоты предполагается, что влияние большинства из них постоянно и неизменно на рассматриваемом временном отрезке. Это позволяет исследовать влияние только двух демографических факторов: численности населения и его возрастного распределения. Сами по себе они не являются причинами преступности, однако влияют на вычисляемые с их использованием показатели учёта преступности.
Одними из основных показателей преступности являются:
1) общее количество преступлений, регистрируемых в стране за год (обозначим его П).
2) и так называемый коэффициент преступности (КП), /1/, показывающий количество преступлений в год, приходящихся на каждую сотню тысяч человек страны, т.е.
 , (4)
, (4)
где Н – среднегодовая численность населения страны.
(Выражение (4) записано в соответствии с методикой Госкомстата России, тогда как в криминологии численность населения при вычислении коэффициента преступности определяется, начиная с возраста уголовной ответственности, т.е. с 14 лет).
4. Многолетние наблюдения за преступностью показывают, что количество преступлений, совершаемых лицами разного возраста, неодинаково. Большое число преступлений совершается в возрасте от 20 до 35 лет. Практически совсем не совершают преступлений лица старше 60-ти лет. Незначительное количество преступных деяний совершается лицами, не достигшими 14 лет, которые, поэтому, не могут рассматриваться как преступники согласно действующему УК России.
Приведём очень грубый пример. Если предположить, что вдруг исчезло всё трудоспособное население (от 14 до 60 лет), то совершать преступления станет практически некому.
Следовательно, показатели преступности зависят как от общей численности населения, так и от относительной численности различных поколений, т.е. распределения населения по возрастам.
На рис. 1 представлено распределение населения России по возрастам, Н (В), на 2000 год. Бросается в глаза его существенная неравномерность. Глубокие демографические “ямы” в возрастном распределении населения России обусловлены драматическими событиями XX века.

Кроме того, общая численность населения в настоящее время уменьшается, причём главным образом за счёт младших поколений. Вследствие этого возрастное распределение населения продолжает деформироваться. Отмеченные тенденции, по-видимому, будут сохраняться и в будущем.
Рис. 1 построен по данным Госкомстата России, /2/. Данные взяты из таблиц. В одном столбце – возрастная группа, в другом – её численность.
Если возрастная группа охватывает собою один полный год возраста, то можно построить такую подробную зависимость Н (В), как на рис. 1 (см. также рис. 7 на стр. 45). Но чаще, для краткости, в одну возрастную группу включают пять лет возраста. При пятилетних возрастных группах человеческая жизнь в пределах 100 лет делится на 20 групп. Будем обозначать через Нi численность i -той пятилетней возрастной группы.
Пусть для того же 2000 года имеются данные о количестве преступлений по возрастам совершивших их лиц П (В), рис. 2, или, если по пятилетним возрастным группам, – Пi.
Тогда можно вычислить несколько важных показателей преступности. Первый – коэффициент преступности, определённый выше выражением (4). Исходные данные для него могут быть определены как
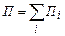 и
и  (5)
(5)
Суммирование в (5) производится по всем пятилетним возрастным группам; i – порядковый номер группы, изменяющийся при суммировании от 1 до 20.
Заметим, что величины П и Н для вычисления коэффициента преступности пропорциональны площадям под кривыми П (В)и Н (В), рис. 2 и рис. 1.
Второй показатель – это распределение отношения количества преступлений, совершённых в каждой i -той возрастной группе населения, к её численности, т.е. возрастные коэффициенты преступности, ВКПi, вычисляемые как
 . (6)
. (6)
Подробная зависимость возрастных коэффициентов преступности от возраста может быть найдена путём деления значения с кривой П (В), рис. 2, на значение с кривой Н (В), рис. 1, для одного и того же года возраста В. В результате получается непрерывная зависимость ВКП (В), представленная на рис. 3.
ВКПi численно равен количеству преступлений, которое в среднем совершает один человек i -той возрастной группы в год.
Рассмотрим некоего усреднённого человека, который с течением времени (жизни) перемещается из одной возрастной группы, i -той, в другую, i +1-ую, затем в следующую, i +2-ую, и т.д.
В i -той пятилетней возрастной группе человек пребывает в течение пяти лет, поэтому среднее количество преступлений, которые он за это время совершает, равно ВКПi × 5. В i +1-ой пятилетней возрастной группе он совершает ВКПi+ 1 × 5 преступлений; в i +2-ой, соответственно – ВКПi+ 2 × 5; и т.д. Сумма этих значений за всю его жизнь даст нам третий показатель преступности, который можно назвать количество преступлений за жизнь (КПЖ), /3/:
 (7)
(7)
(Он вычисляется в предположении, что возрастные коэффициенты преступности различных возрастных групп во время его пребывания в них в течение его жизни совпадают с такими же коэффициентами того года, для которого определяется этот показатель, КПЖ. Величина КПЖ может быть найдена также через площадь под кривой ВКП (В), рис. 3.)
Предположим, что в среднем человек за всю жизнь совершает ровно одно преступление (т.е. КПЖ = 1). Тогда, сравнивая по величине различные ВКПi × 5, можно указать номер возрастной группы, i, в которой совершение этого единственного преступления наиболее вероятно. А, заметив, что сумма всех ВКПi × 5 в этом случае равна единице (КПЖ, (7), = 1), можно рассматривать совокупность величин ВКПi × 5 как закон распределения вероятности. В нём отдельное значение ВКПi × 5 будет численно равно вероятности совершения этого единственного преступления за период времени, пока человек принадлежит к i -той пятилетней возрастной группе, т.е. за пять лет. Обозначим эту вероятность как ВСПi.
 (при КПЖ = 1).
(при КПЖ = 1).
Если человеком совершается за жизнь количество преступлений, отличное от единицы (КПЖ ¹ 1), то вероятность того, что при совершениипреступления человек будет находиться в i -той возрастной группе, ВСПi, необходимо находить так:
 . (8)
. (8)
При этом равенство суммы всех ВСПi единице сохраняется, поскольку это – значения закона распределения вероятности.
В таблицах работы на Excel ВСПi называется вероятностью совершения преступления в данной возрастной группе.
5. Поскольку статистические данные демографии оказывают определённое влияние на вычисляемые с их использованием показатели преступности, в настоящей работе в начале моделируются процессы изменения общей численности населения и численности различных возрастных групп в России в XXI веке, а уже затем производится расчёт показателей преступности, описанных выше.
Перед началом моделирования демографических процессов определим набор переменных, описывающих процесс (см. п. 2).
Для этого всё население разобьём на пятилетние возрастные группы по числу полных лет: от 0 до 4 лет, от 5 до 9 лет, от 10 до 14 лет и так далее до последней группы, в которую включим всех лиц от 85 и старше (объединение групп преклонного возраста допустимо ввиду их малочисленности).
Численность группы от 0 до 4 лет обозначим как Н 0-4(t).
Аналогично обозначим и другие возрастные группы:
Н 5-9(t), Н 10-14(t), …, Н 85-…(t).
На рис. 4 представлено идеализированное распределение численности населения по возрастам, Н (В). (Сравните с реальным на рис. 1.) Возрастная группа от 0 до 4 показана в виде отдельного столбика. Её численность, Н 0-4, равна площади этого столбика.
Процесс изменения численности возрастных групп будем рассматривать через интервал времени Δ t = 5 лет. В качестве начального момента времени выберем t 0 = 2000 год. Начальные значения переменных, которыми являются численности пятилетних возрастных групп, Н 0-4(2000), Н 5-9(2000),…, Н 85-…(2000), возьмём равными тем, которые приводит Госкомстат России, /2/.
Нашей целью будет нахождение последовательности значений численности каждой пятилетней возрастной группы через 5 календарных лет, например:
Н 5-9(2000), Н 5-9(2005), Н 5-9(2010), Н 5-9(2015) и так далее.
Однако для начала моделирования необходимы функции временнòй связи  , (2), для численности каждой возрастной группы. Для их установления будем рассуждать следующим образом.
, (2), для численности каждой возрастной группы. Для их установления будем рассуждать следующим образом.
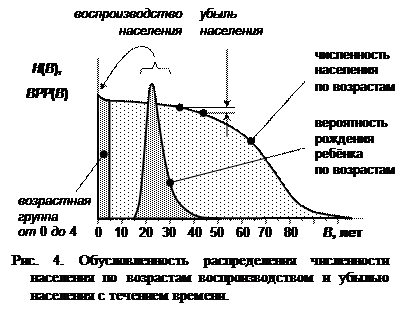
Через пять лет лица каждой пятилетней возрастной группы перемещаются в следующую возрастную группу за исключением тех, кто умер в силу различных причин за эти 5 лет. (Убыль населения выражается в спадании кривой Н (В), рис. 4.) Например, можно записать
Н 5-9(2005) = ВД 0-4 · Н 0-4(2000), (9)
где ВД 0-4– это вероятность дожития человека в возрасте от 0 до 4 полных лет до возраста от 5 до 9.
Для остальных возрастных групп – аналогично:
Н 10-14(2005) = ВД 5-9 · Н 5-9(2000),
Н 15-19(2005) = ВД 10-14 · Н 10-14(2000),
Н 20-24(2005) = ВД 15-19 · Н 15-19(2000),
…,
Н 80-84(2005) = ВД 75-79 · Н 75-79(2000),
Н 85-…(2005) = ВД 80-84 · Н 80-84(2000). (9а)
Величины ВД (*-*) определяются условиями жизни каждой возрастной группы. Для простоты условимся считать их постоянными для любого будущего момента времени. Причём, очевидно, что ВД (*-*)как вероятность не превышает единицу.
Однако полученная модель, (9) и (9а), не является полной, т.к. описывает только убыль населения в различных возрастных группах и не описывает его воспроизводство. Т.е. отсутствует уравнение для Н 0-4(2005).
Количество малолетних детей зависит от ряда показателей:
1) численности женщин детородного возраста (15-49 лет),
2) суммарного коэффициента рождаемости (СКР), т.е. среднего количества детей, рождаемых женщиной за всю жизнь,
3) смертности в раннем детстве.
Кроме того, кривая вероятности рождения ребёнка по возрастам ВРР (В), рис. 4, (на основе данных Госкомстата России, /2/), существенно отличается от равномерной в пределах интервала 15-49 лет. Наиболее вероятным возрастом матери при рождении ребёнка является интервал 20-24 года. Вероятность ребёнку родиться при более позднем возрасте матери меньше.
Поэтому необходимо отдельно рассчитывать вклад в возрастную группу малолетних детей от каждой возрастной группы взрослого населения, а затем суммировать все вклады.
Для описания зависимости репродуктивной активности от возраста в демографии используются возрастные коэффициенты рождаемости, ВКРi, вычисляемые как
 , (10)
, (10)
где НДЕТ i – численность детей, родившихся у женщин i -той пятилетней возрастной группы за год; НЖЕН i – численность женщин i -той возрастной группы.
Общее количество детей, родившихся у женщин всех возрастов за год, выражается так:
 (11)
(11)
ВКРi численно равен количеству детей, которое в среднем рождается у женщины i -той возрастной группы за год.
За время пребывания женщины в i -той пятилетней возрастной группе, т.е. за пять лет, у неё в среднем рождается ВКРi × 5 детей. Количество же детей, которое рождается у женщины за всю жизнь равно сумме таких значений по всем пятилетним возрастным группам и называется суммарным коэффициентом рождаемости (СКР):
 (12)
(12)
СКР – важный обобщающий показатель, который будет использоваться при моделировании. Найдем его место в выражении (11) в явном виде.
Для этого введём (по аналогии с ВСПi (8)) вероятность рождения ребёнка в период времени, пока женщина принадлежит i -той пятилетней возрастной группе, т.е. за пять лет, ВРРi:
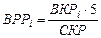 . (13)
. (13)
Сумма ВРРi по всем возрастным группам равна единице.
С учетом введённых обозначений общее количество детей, рождающихся у женщин всех возрастов за год, выражается так:
 . (14)
. (14)
где ВРРi /5 – это вероятность рождения ребёнка в течение одного года у женщины i -той возрастной группы.
С учётом этих рассуждений можно записать искомое уравнение для численности возрастной группы от 0 до 4, в которую входят все дети, рождавшиеся в течение предыдущих пяти лет:
Н 0-4(2005) = 5 · СКР ·((ВРР 15-19 / 5) · Н 15-19(2000) · ДЖ 15-19 +
+ (ВРР 20-24 / 5) · Н 20-24(2000) · ДЖ 20-24 + …
… + (ВРР 45-49 / 5) · Н 45-49(2000) · ДЖ 45-49) · ВВ 0,
(15)
где СКР – суммарный коэффициент рождаемости;
ВРР (*-*) – вероятность рождения ребёнка при пребывании женщины в пределах пятилетней возрастной группы *-*, рис. 4. (Совокупность значений ВРР (*-*) представляет собой закон распределения вероятности рождения ребёнка по пятилетним возрастным группам матери в течение её жизни. В таблицах работы на Excel он именуется как вероятность возраста матери при рождении ребёнка);
Н (*-*) – численность населения в возрастной группе *-*;
ДЖ (*-*) – доля женщин в соответствующей возрастной группе (Из-за опережающей смертности мужчин, см. рис. 7, ДЖ (*-*) до 33 лет – чуть меньше 0,5, а после – чуть больше);
множитель 5 в начале выражения учитывает, что заполнение возрастной группы от 0 до 4 лет происходит в течение 5 лет;
ВВ 0 – вероятность выживания в раннем детстве, усреднённая за 5 лет до заполнения всей возрастной группы от 0 до 4 лет. ВВ 0 = 0,986.
Уравнение (15) достаточно громоздко, и поэтому уже содержится в шаблоне работы на Excel. Кроме того, там уравнение (15) ещё больше упрощено. Опущено умножение и деление на 5. А в связи с тем, что величина ДЖ (*-*)меняется мало, для неё определено некоторое среднее значение ДЖ = 0,497 (соответствующее возрастной группе максимума ВРР (*-*)), которое вынесено за скобки.
Таким образом, получены функции временной связи, необходимые для проведения цепных вычислений по формулам (9), (9а) и (15), см. п. 2. В демографии, /4/, совокупность выражений (9), (9а) и (15) носит название метода возрастных передвижек.
Начальные значения для численностей пятилетних возрастных групп Н (*-*)(2000), а также константы, необходимые в уравнениях (9), (9а) и (15), были взяты или вычислены по данным /2/. В частности, суммарный коэффициент рождаемости в России, снизившись со значения 2,194 в 1987 году до 1,171 в 1999-м, в 2000-м году составил 1,214. (Для сравнения. В областях Центральной России – около 1,1, в Санкт-Петербурге – 0,974. Во Франции – 1,77, в США – 2,02, в Китае – 1,80, в Ираке – 5,25.)
Эти начальные значения и константы, кроме суммарного коэффициента рождаемости, помещены в соответствующие ячейки шаблона работы на Excel.
6. Прогнозирование преступности в работе предлагается сделать при следующих предположениях.
В течение XXI века остаются неизменными и равными их значениям в 2000 году:
– распределение вероятности совершения преступления по возрастным группам, ВСПi, (8);
– количество преступлений, совершаемых одним человеком в течение жизни, КПЖ, (7).
Это оправдано, т.к. криминологические исследования показывают высокое постоянство значений закона распределения ВСПi. А КПЖ представляет собой обобщающий показатель действия всей совокупности причин, приводящих к совершению преступлений. Задавая постоянство КПЖ, в определённом смысле, задаётся постоянство степени криминогенности условий жизни, т.к. сейчас с определённостью предсказать направление их изменения в будущем не представляется возможным.
Распределение вероятности совершения преступления по возрастным группам, ВСПi, взято из /1; стр. 277/.
Значение количества преступлений, совершаемых человеком за всю жизнь, КПЖ, в исходном 2000 году будет определено при выполнении работы путём подбора. Расчёты, проведённые с использованием этого значения, для 2000 года должны давать то же общее количество преступлений П, что и приведённое в статистике МВД по России, /5/, а именно: 2952 тысячи зарегистрированных преступлений (вопросы сокрытия преступлений, а также различия их по степени тяжести здесь не рассматриваем).
Кроме того, в течение XXI века считаются неизменными и равными их значениям в 2000 году все демографические показатели: вероятности дожития до следующей возрастной группы ВД (*-*), доля женщин ДЖ, вероятности рождения ребёнка в пределах каждой возрастной группы ВРР (*-*) и вероятность выживания в раннем детстве ВВ 0. Суммарный коэффициент рождаемости СКР также считается неизменным, а его значение будет определяться исходя из номера варианта.
Помимо смертности и рождаемости численность населения существенно зависит также от миграционных процессов, которые, однако, для простоты в настоящей работе не учитываются. (Более полный демографический прогноз до 2016 года см. в /4/, а до 2050 года – в издании Центра демографии и экологии человека, /6/.)
Таким образом, прогнозное моделирование производится в предположении «если всё, как сейчас». В итоге должны быть получены процессы изменения в течение XXI века
- распределения количества преступлений по возрастам Пi (выражение (16) ниже);
- общего количества преступлений П, (5);
- коэффициента преступности КП, (4).
Выведем выражение, необходимое для расчёта количества преступлений, совершённых за год в каждой пятилетней возрастной группе, Пi.
Из (6) выразим искомую величину:
 ,
,
где Чi берётся из демографических расчётов для того же года и той же пятилетней возрастной группы, для которой рассчитывается Пi; а ВКПi выражается из (8):
 ,
,
где КПЖ определяется подбором в ходе работы, а ВСПi дано.
Следовательно, количество преступлений, совершённых в пятилетней возрастной группе *-*, вычисляется так:
П (*-*) = (КПЖ · ВСП (*-*) / 5)· Н (*-*). (16)
Общее количество преступлений, совершённых за год, согласно (5), находится путём суммирования преступлений всех возрастных групп, (16):
П = П 10-14 + П 15-19 + П 20-24+ … + П 85-…. (17)
Дата добавления: 2015-10-24; просмотров: 87 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Статья... Административные правонарушения в области градостроительной деятельности на территории _____________ (наименование субъекта Российской Федерации). | | | Порядок выполнения |