
Читайте также:
|
Таблица 1
| Поступательное движение | Вращательное движение | |
| КИНЕМАТИКА Равномерное движение | ||
Путь  , м
Скорость , м
Скорость  , м/с
Ускорение , м/с
Ускорение  , м/с2 , м/с2
| Угловой путь  , рад
Угловая скорость , рад
Угловая скорость 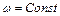 , рад/с
Угловое ускорение , рад/с
Угловое ускорение  , рад/с2 , рад/с2
| |
| Равнопеременное движение | ||



| 


| |
| Произвольное движение | ||

 Тангенциальное ускорение
Тангенциальное ускорение  Нормальное ускорение
Нормальное ускорение 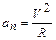
 – радиус кривизны траектории
Полное ускорение – радиус кривизны траектории
Полное ускорение 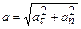
| 


| 


 – радиус окружности – радиус окружности
|
| ДИНАМИКА Основные величины | ||
Масса тела  , кг
Сила , кг
Сила  , н
Сила тяжести , н
Сила тяжести  Ускорение свободного
падения
Ускорение свободного
падения  , м/с2
Сила упругости , м/с2
Сила упругости  , ,
 – коэффициент жесткости – коэффициент жесткости
 – величина деформации
Сила трения – величина деформации
Сила трения 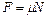 , ,
 – коэффициент трения – коэффициент трения
 – сила реакции опоры – сила реакции опоры
| Момент инерции  , кг·м2
Для некоторых тел относительно оси симметрии
Тонкий стержень длины , кг·м2
Для некоторых тел относительно оси симметрии
Тонкий стержень длины  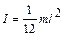 Сплошной диск (цилиндр)
Сплошной диск (цилиндр)  Шар
Шар 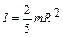 Момент силы
Момент силы  , н·м , н·м
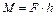 , ,
 – плечо силы – расстояние от оси до линии действия силы – плечо силы – расстояние от оси до линии действия силы 
|
Продолжение таблицы 1
Импульс тела  , ,  Работа силы
Работа силы  , Дж
Работа переменной силы , Дж
Работа переменной силы  Кинетическая энергия тела
Кинетическая энергия тела  Потенциальная энергия тела:
1). в поле тяжести:
а).
Потенциальная энергия тела:
1). в поле тяжести:
а).   б).
б).  – любое – любое  , ,
 – масса и радиус Земли – масса и радиус Земли
 – гравитационная постоянная
2). в поле упругих сил – гравитационная постоянная
2). в поле упругих сил 
| Момент импульса  Для вращающегося тела
Для вращающегося тела  , ,  Работа момента силы
Работа момента силы  , Дж , Дж
 Кинетическая энергия вращающегося тела
Кинетическая энергия вращающегося тела

|
| Законы | |
Второй закон Ньютона  Закон сохранения импульса
Закон сохранения импульса 
| Основной закон динамики вращательного движения  Закон сохранения момента импульса
Закон сохранения момента импульса 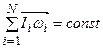
|
Закон сохранения энергии в механике

| |
| ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ | |
Уравнение гармонических колебаний 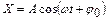 Вид силы, вызывающий гармонические колебания
Вид силы, вызывающий гармонические колебания
 ; ;  Полная энергия колеблющейся материальной точки массы
Полная энергия колеблющейся материальной точки массы 
 ; ; 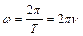 ,
где ,
где  – смещение; – смещение;  – амплитуда колебания ( – амплитуда колебания ( ); );
 – фаза колебания; – фаза колебания;  – начальная фаза; – начальная фаза;
 – циклическая частота; – циклическая частота;  – период колебаний; – период колебаний;  – частота.
Период колебаний физического маятника – частота.
Период колебаний физического маятника
 ,
где ,
где  – момент инерции маятника относительно оси колебаний; – момент инерции маятника относительно оси колебаний;
 – расстояние от оси колебаний до центра тяжести; – расстояние от оси колебаний до центра тяжести;
 – ускорение свободного падения; – ускорение свободного падения;  – масса маятника. – масса маятника.
|
Пример1. Колесо вращается с постоянным угловым ускорением

 . Через
. Через  после начала движения полное ускорение точек обода колеса
после начала движения полное ускорение точек обода колеса  . Найти радиус колеса.
. Найти радиус колеса.
Дано:  ;
;  ;
;
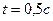 ;
;
 .
.
Найти:  .
.
Рисунок 1.
Решение. Полное ускорение точек обода  .
.
Отсюда  . (1.1)
. (1.1)
Нормальное ускорение  .
.
Так как движение равнопеременное ( ,
,  ),
),
то  .
.
В нашем случае  и
и  .
.
Таким образом  .
.
Тангенциальное ускорение связано с угловым
 . (1.2)
. (1.2)
Тогда  . (1.3)
. (1.3)
Подставим формулы (1.2) и (1.3) в формулу (1.1):
 .
.
Отсюда  .
.
Подставляя заданные численные значения величин, получим
 .
.
Пример 2. Молот массой  ударяет по небольшому куску мягкого железа, лежащему на наковальне. Масса наковальни
ударяет по небольшому куску мягкого железа, лежащему на наковальне. Масса наковальни  . Определить
. Определить
к. п. д. удара молота при данных условиях. Удар считать неупругим. Полезной в данном случае является энергия, пошедшая на деформацию куска железа.
Дано:  ;
;  т
т  .
.
Найти:  .
.
Решение. По определению
 (2.1)
(2.1)
В нашем случае затраченная работа равна кинетической энергии молота перед ударом
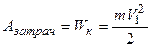 , (2.2)
, (2.2)
где 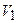 – скорость молота непосредственно перед ударом по железу.
– скорость молота непосредственно перед ударом по железу.
Полезная же работа по закону сохранения энергии равна разности между кинетической энергией молота до удара и кинетической энергией системы – молот + наковальня – после удара.
 . (2.3)
. (2.3)
Массой небольшого куска железа пренебрегаем. Для определения скорости  молота и наковальни после удара воспользуемся законом сохранения импульса.
молота и наковальни после удара воспользуемся законом сохранения импульса.
В нашем случае имеем
 .
.
В скалярном виде
 .
.
Отсюда  .
.
Подставляя это выражение в формулу (2.3), получим
 . (2.4)
. (2.4)
Подставим формулы (2.4) и (2.2) в исходную формулу (2.1)
 .
.
Подставим численное значение величин
 ;
;  .
.
Пример 3. Через неподвижный блок массой  перекинут шнур, к концам которого подвешены грузы массами
перекинут шнур, к концам которого подвешены грузы массами  и
и  .
.
 Определить силы натяжения шнура
Определить силы натяжения шнура  и
и  по обе стороны блока во время движения грузов, если массу блока можно считать равномерно распределенной по ободу.
по обе стороны блока во время движения грузов, если массу блока можно считать равномерно распределенной по ободу.
Дано:  ;
;  ;
;  .
.
Найти:  ,
,  .
.
Решение. Два тела  и
и  движутся поступательно. Воспользуемся вторым законом Ньютона
движутся поступательно. Воспользуемся вторым законом Ньютона
 .
.
Для первого тела имеем
 . Рисунок 2.
. Рисунок 2.
В скалярном виде (выбираем положительным направление движения вверх)
 . (3.1)
. (3.1)
Для второго тела
 .
.
Выбираем положительным направление движения вниз
 . (3.2)
. (3.2)
Мы учли, что 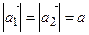 .
.
Третье тело – блок – вращается.
Воспользуемся основным законом динамики вращательного движения
 .
.
В нашем случае
 .
.
Считая положительным направление вращения по часовой стрелке, получаем
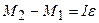 .
.
Учитывая, что
 ;
;  ;
;  ;
;  ,
,
получаем  ,
,
то есть  .
.
Согласно третьему закону Ньютона с учетом невесомости шнура
 и
и  .
.
Таким образом
 (3.3)
(3.3)
 Итак, получили систему трех уравнений с тремя неизвестными:
Итак, получили систему трех уравнений с тремя неизвестными:  и
и  .
.
 ,
,
 ,
,
 .
.
Сложив, соответственно, левые и правые стороны уравнений, находим
 .
.
Отсюда
 . (3.4)
. (3.4)
Подставляя формулу (3.4) в первое уравнение системы, находим
 .
.
После подстановки численных значений
 (н).
(н).
Соответственно, второе уравнение системы с учетом формулы (3.4) примет вид
 .
.
 (н).
(н).
Пример 4. На краю горизонтальной платформы, имеющей форму диска радиусом 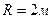 , стоит человек. Масса платформы
, стоит человек. Масса платформы  , масса человека
, масса человека  . Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью
. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью

 относительно платформы.
относительно платформы.
Дано: 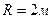 ;
;
 ;
;
 ;
;
 .
.
Найти:  .
.
Рисунок 3.
Решение. Воспользуемся законом сохранения момента импульса
 .
.
В нашем случае  ,
,
так как в начале ни человек, ни платформа не двигались.
В скалярном виде, считая положительным направление движения человека, получим
 . (4.1)
. (4.1)
Моменты инерции человека  и платформы
и платформы  относительно оси вращения, соответственно, равны
относительно оси вращения, соответственно, равны
 ;
;  . (4.2)
. (4.2)
Угловая скорость  человека относительно Земли есть
человека относительно Земли есть

и так как 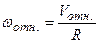 ,
,
то  . (4.3)
. (4.3)
Подставим формулы (4.3) и (4.2) в формулу (4.1)
 .
.
Отсюда  .
.
Подставляем численные значения
 .
.
Пример 5. Вагон массой  движется на упор со скоростью
движется на упор со скоростью
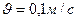 . При полном торможении вагона буферные пружины сжимаются на
. При полном торможении вагона буферные пружины сжимаются на  . Определить максимальную силу
. Определить максимальную силу  сжатия буферных пружин и продолжительность
сжатия буферных пружин и продолжительность  торможения.
торможения.
Дано:  т
т  ;
;
 ;
;  .
.
Найти:  и
и  .
.
Решение. При сжатии пружин сила сжатия определяется их силой упругости  ,
,
где  – величина сжатия;
– величина сжатия; 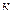 – коэффициент жесткости пружин.
– коэффициент жесткости пружин.
Соответственно, искомая сила максимального сжатия
 . (5.1)
. (5.1)
По закону сохранения энергии кинетическая энергия вагона при остановке перейдет в потенциальную энергию сжатия пружин
 .
.
Отсюда  .
.
Подставляя выражение для «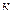 » в формулу (5.1), получим
» в формулу (5.1), получим
 .
.
Вычисляем  .
.
Для нахождения времени сжатия пружин используем то, что под действием сил упругости смещение  вагона определяется гармоническим законом
вагона определяется гармоническим законом
 ,
,
а скорость вагона соответственно
 .
.
 В начальный момент сжатия
В начальный момент сжатия  было
было
 ,
,
 .
.
Отсюда
 ;
;  . (5.3)
. (5.3)
При остановке через  имеем
имеем

 ,
,
 .
.
Отсюда
 . (5.4)
. (5.4)
 . (5.5)
. (5.5)
Подставляя в формулу (5.4) выражение (5.3) с учетом формулы (5.5) получим  .
.
Окончательно  .
.
 .
.
Пример 6. На концах стержня массой 1 кг и длиной 40 см укреплены одинаковые грузы массами 400 г по одному на каждом конце. Стержень с грузами колеблется около оси, проходящей через точку, удаленную на 10 см от одного из концов стержня. Определить период колебаний стержня.
 Дано:
Дано:  ;
;
 ;
;
 ;
;
 .
.
Найти: 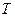 .
.
Рисунок 4.
Решение. Период колебаний физического маятника (а это – любое тело, колеблющееся около оси, не проходящей через центр тяжести) определяется формулой
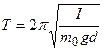 , (6.1)
, (6.1)
где  – расстояние от оси колебаний до центра тяжести маятника. В нашем случае
– расстояние от оси колебаний до центра тяжести маятника. В нашем случае
 . (6.2)
. (6.2)
 – общая масса маятника.
– общая масса маятника.
 . (6.3)
. (6.3)
 – ускорение свободного падения.
– ускорение свободного падения.
 – момент инерции маятника относительно оси колебаний
– момент инерции маятника относительно оси колебаний
 . (6.4)
. (6.4)
Моменты инерции грузиков, как материальных точек, равны
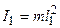 ;
;  . (6.5)
. (6.5)
Моменты инерции стержня находим, используя теорему Штейнера-Гюйгенса  .
.
Момент инерции  стержня относительно оси, проходящей через центр тяжести, равен
стержня относительно оси, проходящей через центр тяжести, равен  и, значит,
и, значит,
 . (6.6)
. (6.6)
Подставляя формулы (6.5) и (6.6) в выражение (6.4) находим
 .
.
И, подставляя это выражение вместе с формулой (6.3) в выражение (6.1), окончательно получаем
 .
.
Вычисляем  .
.
 .
.
Задачи
1.01. Колесо радиусом  вращается согласно уравнению
вращается согласно уравнению
 , где
, где 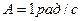 ;
;  . Определить полное ускорение точек на окружности колеса в момент времени
. Определить полное ускорение точек на окружности колеса в момент времени  .
.
1.02. Движения двух материальных точек выражаются уравнениями
 и
и  , где
, где  ;
;  ;
;  ;
;
 ;
;  ;
;  . В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент?
. В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент?
1.03. Материальная точка движется по окружности радиуса 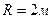 согласно уравнению
согласно уравнению  , где
, где  ;
;  . Найти скорость
. Найти скорость  , тангенциальное
, тангенциальное 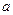 τ, нормальное
τ, нормальное  и полное
и полное 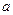 ускорения в момент времени
ускорения в момент времени
 .
.
1.04. Материальная точка движется прямолинейно. Уравнение движения имеет вид  , где
, где  ;
;  . Найти скорость
. Найти скорость  и ускорение точки в моменты времени
и ускорение точки в моменты времени  и
и  . Каковы средние значения скорости и ускорения за первые
. Каковы средние значения скорости и ускорения за первые  движения?
движения?
1.05. Точка движется по прямой согласно уравнению  , где
, где
 ;
;  . Определить среднюю скорость
. Определить среднюю скорость  точки в интервале времени от
точки в интервале времени от  до
до  .
.
1.06. Две материальные точки движутся согласно уравнениям и  , где
, где  ;
;  м/с;
м/с;  ;
;  ;
;  ,
,  . В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в этот момент?
. В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в этот момент?
1.07. Диск радиусом  вращается согласно уравнению
вращается согласно уравнению 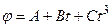 , где
, где  ;
; 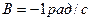 ;
;  . Определить тангенциальное
. Определить тангенциальное  , нормальное
, нормальное  и полное
и полное 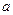 ускорения точек на окружности диска для момента времени
ускорения точек на окружности диска для момента времени 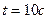 .
.
1.08. По дуге окружности радиуса  вращается точка. В некоторый момент времени нормальное ускорение точки
вращается точка. В некоторый момент времени нормальное ускорение точки  , вектор полного ускорения образует в этот момент с вектором нормального ускорения угол
, вектор полного ускорения образует в этот момент с вектором нормального ускорения угол  . Найти скорость
. Найти скорость  и тангенциальное ускорение
и тангенциальное ускорение  точки.
точки.
1.09. Точка движется по окружности с  с тангенциальным ускорением
с тангенциальным ускорением  . Через сколько времени после начала движения нормальное ускорение
. Через сколько времени после начала движения нормальное ускорение  станет вдвое больше тангенциального.
станет вдвое больше тангенциального.
1.10. Колесо вращается так, что зависимость угла поворота колеса от времени дается уравнением  , где
, где  ,
,  и
и  . Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, равно
. Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, равно  .
.
1.11. Тело массой 3 кг поднимают вертикально с ускорением 4м/с2. При этом совершается работа 126 Дж. На какую высоту подняли тело?
1.12. К шнуру подвешена гиря. Гирю отвели в сторону так, что шнур принял горизонтальное положение, и отпустили. Масса гири 0,5 кг. Определить силу натяжения в момент прохождения гирей положения равновесия.
1.13. Абсолютно упругий шар массой  сталкивается с покоящимся упругим шаром большей массы. В результате центрального прямого удара шар потерял 36% своей кинетической энергии. Определить массу m2 большего шара.
сталкивается с покоящимся упругим шаром большей массы. В результате центрального прямого удара шар потерял 36% своей кинетической энергии. Определить массу m2 большего шара.
1.14. Боек свайного молота массой  падает с некоторой высоты на сваю массой
падает с некоторой высоты на сваю массой  . Найти к. п. д. бойка, считая удар неупругим. Полезной считать энергию, пошедшую на углубление сваи.
. Найти к. п. д. бойка, считая удар неупругим. Полезной считать энергию, пошедшую на углубление сваи.
1.15. Шарик массой  свободно падает с высоты
свободно падает с высоты  на стальную плиту и подпрыгивает на высоту
на стальную плиту и подпрыгивает на высоту  . Определить импульс р (по величине и направлению), сообщенный плитой шарику.
. Определить импульс р (по величине и направлению), сообщенный плитой шарику.
1.16. Шар массой 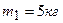 движется со скоростью
движется со скоростью  и сталкивается с покоящимся шаром массой
и сталкивается с покоящимся шаром массой  . Вычислить работу A, совершенную при деформации шаров при прямом центральном ударе. Шары считать неупругими.
. Вычислить работу A, совершенную при деформации шаров при прямом центральном ударе. Шары считать неупругими.
1.17. Атом распадается на две части массами  и
и
 . Определить кинетические энергии T1и Т2частей атома, если их общая кинетическая энергия
. Определить кинетические энергии T1и Т2частей атома, если их общая кинетическая энергия  . Кинетической энергией и импульсом атома до распада пренебречь.
. Кинетической энергией и импульсом атома до распада пренебречь.
1.18. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на  . На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты
. На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты  ?
?
1.19. Из ствола автоматического пистолета вылетела пуля массой  со скоростью
со скоростью 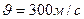 . Затвор пистолета массой
. Затвор пистолета массой  прижимается к стволу пружиной, жесткость которой
прижимается к стволу пружиной, жесткость которой  . На какое расстояние отойдет затвор после выстрела? (Считать, что пистолет жестко закреплен.)
. На какое расстояние отойдет затвор после выстрела? (Считать, что пистолет жестко закреплен.)
1.20. Две пружины жесткостью  и
и  скреплены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина была растянута на
скреплены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина была растянута на  .
.
1.21. Диск радиусом  и массой
и массой 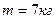 вращается согласно уравнению
вращается согласно уравнению 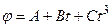 , где
, где  ;
; 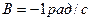 ;
;  . Найти закон, по которому меняется вращающий момент, действующий на диск. Определить этот момент сил М в момент времени
. Найти закон, по которому меняется вращающий момент, действующий на диск. Определить этот момент сил М в момент времени  .
.
1.22. Маховик радиусом  насажен на горизонтальную ось. На обод маховика намотан шнур, к которому привязан груз массой
насажен на горизонтальную ось. На обод маховика намотан шнур, к которому привязан груз массой  . Опускаясь равноускоренно, груз прошел расстояние
. Опускаясь равноускоренно, груз прошел расстояние  за время
за время  . Определить момент инерции J маховика.
. Определить момент инерции J маховика.
1.23. Через блок радиусом  перекинули шнур, к концам которого привязаны грузы массами
перекинули шнур, к концам которого привязаны грузы массами  и
и 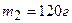 . При этом грузы пришли в движение с ускорением
. При этом грузы пришли в движение с ускорением  . Определить момент инерции блока. Трение при вращении не учитывать.
. Определить момент инерции блока. Трение при вращении не учитывать.
1.24. Тонкий стержень длиной  и массой
и массой  вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение вращения стержня
вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение вращения стержня  , где
, где 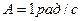 ;
;  . Определить вращающий момент М в момент времени
. Определить вращающий момент М в момент времени  .
.
1.25. Шарик массой  , привязанный к концу нити длиной
, привязанный к концу нити длиной  , вращается с частотой
, вращается с частотой  , опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния
, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния  .
.
С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
1.26. Платформа в виде диска радиусом  вращается по инерции с частотой
вращается по инерции с частотой  . На краю платформы стоит человек, масса которого
. На краю платформы стоит человек, масса которого
 , С какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы
, С какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы  . Момент инерции человека рассчитывать, как для материальной точки.
. Момент инерции человека рассчитывать, как для материальной точки.
1.27. Человек стоит на скамье Жуковского и ловит рукой мяч массой
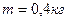 , летящий в горизонтальном направлении со скоростью
, летящий в горизонтальном направлении со скоростью  . Траектория мяча проходит на расстоянии
. Траектория мяча проходит на расстоянии  от вертикальной оси вращения скамья. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамейки
от вертикальной оси вращения скамья. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамейки  .
.
1.28. Обруч и диск одинаковой массы катятся без скольжения с одинаковой линейной скоростью. Кинетическая энергия обруча  . Найти кинетическую энергию
. Найти кинетическую энергию  диска.
диска.
1.29. Сплошной цилиндр скатился с наклонной плоскости высотой
 . Определить скорость
. Определить скорость  поступательного движения цилиндра в конце наклонной плоскости.
поступательного движения цилиндра в конце наклонной плоскости.
1.30. Сплошной однородный диск катится по горизонтальной плоскости со скоростью  . Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен 0,02.
. Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен 0,02.
1.31. Амплитуда гармонического колебания 5 см, период 4 сек. Найти максимальную скорость колеблющейся точки и ее максимальное ускорение.
1.32. Тонкий обруч радиусом 40 см подвешен на нити длиной 20 см. Определить частоту колебаний такого маятника.
1.33. Амплитуда колебаний материальной точки 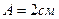 , полная энергия
, полная энергия  . При каком смещении от положения равновесия на колеблющуюся точку действует сила
. При каком смещении от положения равновесия на колеблющуюся точку действует сила  ?
?
1.34. Толстостенное кольцо с радиусами  и
и  колеблется около горизонтальной оси, отстоящей от центра кольца на расстоянии
колеблется около горизонтальной оси, отстоящей от центра кольца на расстоянии  . Определить период колебаний такого маятника.
. Определить период колебаний такого маятника.
1.35. Определить полную энергию точки массой 20 г, совершающей гармонические колебания  , а также определить силу, действующую на точку в момент времени
, а также определить силу, действующую на точку в момент времени  .
.
1.36. Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину радиуса перпендикулярно к плоскости диска. Определить частоту колебаний такого маятника.
1.37. Амплитуда колебаний материальной точки 5 см, период 0,2 с, начальная фаза равна  . Какова скорость точки в тот момент, когда ее смещение равно 3 см?
. Какова скорость точки в тот момент, когда ее смещение равно 3 см?
1.38. Шар радиуса 40 см колеблется около оси, проходящей горизонтально через шар на расстоянии 30 см от центра шара. Найти период колебаний этого маятника.
1.39. Написать уравнение гармонических колебаний точки, если ее максимальное ускорение равно 0,5 м/с2, период колебаний 2 сек. И смещение точки от положения равновесия в начальный момент времени равно 2,5 см.
1.40. Стержень длиной 2 м колеблется около оси, проходящей на расстоянии 0,4 м от одного из концов. Найти период колебаний стержня.
Дата добавления: 2015-10-24; просмотров: 176 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение задач | | | Основные физические величины и законы |