
|
Читайте также: |
Аралыєында берілген функциясыныѕ алєашќы функциясы
 //
//  //
//
E) 
Интегралына Эйлер алмастыруын ќолдану жолдары
C)  болса,
болса, 
E)  болса,
болса, 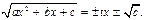
H) 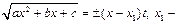 квадрат їшмїшеліктіѕ наќты тїбірі
квадрат їшмїшеліктіѕ наќты тїбірі
 теѕдігі дўрыс болатындай F(x):
теѕдігі дўрыс болатындай F(x):
A) 
C) 
E) 
 теѕдігі дўрыс болатындай F(x):
теѕдігі дўрыс болатындай F(x):
 //
// 

 теѕдігі дўрыс болатындай F(x):
теѕдігі дўрыс болатындай F(x):
B) 
D) 
F) 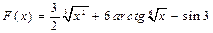
 жиыны їшін орындалатын ќатынас:
жиыны їшін орындалатын ќатынас:
A)  D)
D) 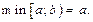
G) 
 - сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
- сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
C) шегі 0-ге теѕ
G) 1саны жоєарєы шекара
H) 0 саны тґменгі шекара
 - сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
- сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
A)  E)
E) 
H) 
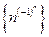 - сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
- сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
A) шегі жоќ F) жоєарыдан шенелмеген
G) аќырсыз їлкен емес
 - сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
- сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
 //
// 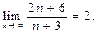

 - сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
- сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
C) 
D) жинаќты G) фундаментальды тізбек
 - сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
- сандыќ тізбегіне ќатысты келесі пікірлер орындалады:
A) фундаментальды тізбек E) жинаќты
H) 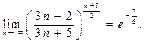
 сандыќ тізбегі їшін келесі пікірлер орындалады:
сандыќ тізбегі їшін келесі пікірлер орындалады:
C) жинаќты D) шенелген E) 
нїктесі функцияcыныѕ 2 текті їзіліс нїкте болуы їшін келесі шарттыѕ орындалуы жеткілікті
A) 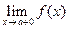 оѕ жаќ шегі жоќ
оѕ жаќ шегі жоќ
B)  сол жаќ шегі жоќ
сол жаќ шегі жоќ
F) 
 нїктесі
нїктесі  функцияcыныѕ 1 – текті їзіліс нїкте болса, онда:
функцияcыныѕ 1 – текті їзіліс нїкте болса, онда:
C) 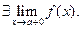 D)
D) 
G) 
 мен
мен 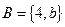 жиындарыныѕ айырымын кґрсететін ґрнек:
жиындарыныѕ айырымын кґрсететін ґрнек:
C)  D)
D)  G)
G) 
 мен
мен 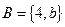 жиындарыныѕ бірігуін кґрсететін ґрнек:
жиындарыныѕ бірігуін кґрсететін ґрнек:
A)  C)
C)  E)
E) 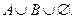
 мен
мен 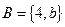 жиындарыныѕ ќиылысуын кґрсететін ґрнек:
жиындарыныѕ ќиылысуын кґрсететін ґрнек:
B)  C)
C) 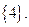 F)
F) 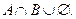
A мен B жиындарыныѕ бірігуін кґрсететін ґрнек:
 //
//  //
// 
A мен B жиындарыныѕ ќиылысуын кґрсететін ґрнек:
 //
//  //
// 
A мен B жиындарыныѕ симметриялыќ айырымын кґрсететін ґрнек:
(B\A)  (A\B)//
(A\B)//  // B\ A.
// B\ A.
 їшін Ролль теоремасыныѕ шарты орындалатын аралыќтар:
їшін Ролль теоремасыныѕ шарты орындалатын аралыќтар:
 //
//  //
// 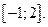
 функциясы їшін Ролль теоремасыныѕ шарты орындалатын аралыќтар:
функциясы їшін Ролль теоремасыныѕ шарты орындалатын аралыќтар:
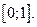 //
//  //
// 
 функциясына байланысты ќасиеттер мен теѕдіктер:
функциясына байланысты ќасиеттер мен теѕдіктер:
B) 
 D)
D) 
F) 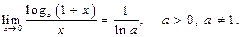
 функциясы їшін:
функциясы їшін:
B) 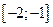 кесіндіде Ролль теоремасыныѕ шарты орындалады
кесіндіде Ролль теоремасыныѕ шарты орындалады
E)  кесіндіде Лагранж теоремасыныѕ шарты орындалады
кесіндіде Лагранж теоремасыныѕ шарты орындалады
G)  кесіндіде Ролль теоремасыныѕ шарты орындалады
кесіндіде Ролль теоремасыныѕ шарты орындалады
 функциясыныѕ алєашќы функциясы:
функциясыныѕ алєашќы функциясы:
A)  -
-
E) 
H) 
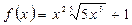 функциясыныѕ алєашќы функциясы:
функциясыныѕ алєашќы функциясы:
B) 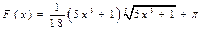
E) 
F) 
 функциясыныѕ алєашќы функциясы:
функциясыныѕ алєашќы функциясы:
A) 
B) 
D) 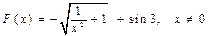
 функциясыныѕ алєашќы функциясы:
функциясыныѕ алєашќы функциясы:
B) 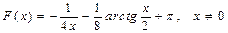
C) 
D) 
 функциясы берілген
функциясы берілген 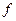 функциясыныѕ алєашќы функциясы болуы їшін:
функциясыныѕ алєашќы функциясы болуы їшін:
A)  функциясы
функциясы  кесіндісінде їзіліссіз болуы ќажет
кесіндісінде їзіліссіз болуы ќажет
E)  нїктелерінде
нїктелерінде  туындысы бар болуы ќажет
туындысы бар болуы ќажет
H)  нїктелерінде
нїктелерінде  теѕдігі орындалуы ќажет
теѕдігі орындалуы ќажет  шегіне ќатысты орындалатын тўжырым:
шегіне ќатысты орындалатын тўжырым:
B) 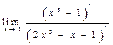 шегі бар
шегі бар
C)  D)
D) 
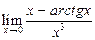 шегіне ќатысты орындалатын тўжырымдар:
шегіне ќатысты орындалатын тўжырымдар:
B)  шегі бар
шегі бар
C) 
F) 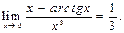
 шегіне ќатысты орындалатын тўжырымдар:
шегіне ќатысты орындалатын тўжырымдар:
A)  шегі бар
шегі бар
C) 
H) 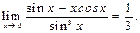
 шегіне ќатысты орындалатын тўжырымдар:
шегіне ќатысты орындалатын тўжырымдар:
B) 



D) 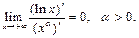
E) 
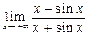 шегіне ќатысты дўрыс тўжырымдар:
шегіне ќатысты дўрыс тўжырымдар:
A) Лопиталь ережесін ќолдана алмаймыз
D)  шегі жоќ
шегі жоќ
F) 
 нїктесінде туындысы жоќ функциялар:
нїктесінде туындысы жоќ функциялар:
A) 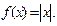 F) ƒ
F) ƒ  H)
H) 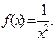
U жиыныныѕ ішкі жиындары A мен B – ныѕ бірігуін кґрсететін ґрнек:
 //
//  //
// 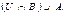
U жиыныныѕ ішкі жиындары A мен B – ныѕ ќиылысуын кґрсететін ґрнек:

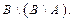

U жиыныныѕ ішкі жиындары A мен B – ныѕ айырымын кґрсететін ґрнек:
D) A\ (A  U) E)
U) E)  F )
F ) 
Бос жиынды кґрсететін ґрнек:
C)  D)
D)  H)
H) 
Егер  саны Е жиыныныѕ дјл тґменгі шекарасы болса, онда:
саны Е жиыныныѕ дјл тґменгі шекарасы болса, онда:
A) 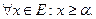
F) 
G) 
Егер  -саны Е жиыныныѕ дјл жоєарєы шекарасы болса, онда:
-саны Е жиыныныѕ дјл жоєарєы шекарасы болса, онда:
B) 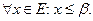
E) 
H) 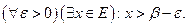
Егер  сандыќ тізбектіѕ шегі а теѕ болса, онда:
сандыќ тізбектіѕ шегі а теѕ болса, онда:
A)  D)
D)  -шенелген тізбек
-шенелген тізбек
G)  - фундаментальды тізбек
- фундаментальды тізбек
Егер  сандыќ тізбектіѕ шегі а болса, онда:
сандыќ тізбектіѕ шегі а болса, онда:
B) 
D) 
G)  - фундаментальды тізбек
- фундаментальды тізбек
Егер  нїктесі
нїктесі  функцияcы їшін їзіліс нїкте болса, онда:
функцияcы їшін їзіліс нїкте болса, онда:
B) 
C) 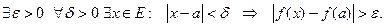
H) Ол, бірінші немесе екінші текті їзіліс нїкте
Дата добавления: 2015-10-24; просмотров: 132 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| УПАДОК ИСТОРИИ 4 страница | | | Егер В жиыны А жиыныныѕ ішкі жиыны болса, онда |