Егер В жиыны А жиыныныѕ ішкі жиыны болса, онда

// //

Егер функциясы 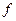функциясыныѕ аралыєындаєы алєашќы функциясы болса, онда:

B)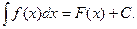

E) аралыєыныѕ ішкі нїктелерінде

F) 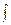f(X)dx, k – тўраќты

Егер 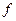функцияларыныѕ нїктесінде туындысы бар болса, онда:

C) E) периодты функция

G)

Егер f функциясы аралыєында ґспелі болса, онда:

B)

D)

G) f жоєарыдан шенелмеген жаєдайда

Егер f функциясы аралыєында кемімелі болса, онда:

//

F) f тґменнен шенелмеген жаєдайда

Егер 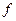функцияcы кесіндісінде їзіліссіз болса, онда:

C) осы кесіндіде оныѕ еѕ їлкен мјні бар

E) осы кесіндіде оныѕ еѕ кіші мјні бар

H) осы кесіндіде ол шенелген

Егер 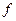функцияcы нїктеде їзіліссіз болса, онда:

Егер 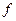жјне g функциялары нїктеде їзіліссіз болса, онда:

А) функциясы нїктеде їзіліссіз

C) функциясы нїктеде їзіліссіз

G) 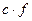(с – тўраќты) функциясы нїктеде їзіліссіз

Егер ƒ(x), g(x), h(x) - функциялары нїктесінде дифференциалданса, онда:

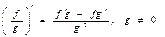
Егер берілсе, онда::

C) жўп функция D)

F) функция нїктеде аныќталмаєан

Егер берілсе, онда:

A) C) жўп функция.

H) функциясы нїктесініѕ маѕайында шенелген

Егер берілсе, онда:

B) - їзіліссіз функция

C)

F) - функцияныѕ жойылатын їзіліс нїктесі

Егер берілсе, онда:

B) оныѕ нїктесіндегі жанамасы:

F)

G) аралыєында дифференциалданады

Егер берілсе, онда::

C) шегі жоќ E) таќ функция

H) шенелген функция

Егер берілсе, онда:

A) - функцияныѕ 2-текті їзіліс нїктесі

B) нїктелерінде функция їзіліссіз

E) нїктелерінде функция їзіліссіз

Егер берілсе, онда:

C)

E) ол аралыєында їзіліссіз

G)

Егер 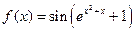берілсе, онда:

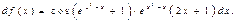
C)

D) ол аралыєында їзіліссіз

Егер берілсе, онда:

жоќ// жоќ

ол аралыєында їзіліссіз

Егер 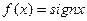берілсе, онда:

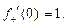
таќ функция

Егер 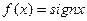берілсе, онда:

// шегі жоќ

Егер 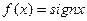берілсе, онда:

B) - функцияныѕ 1текті їзіліс нїктесі

D)

F) таќ функция

Егер 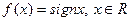функциясы берілсе, онда:

A) оныѕ алєашќы функциясы бар

D) - оныѕ їзіліс нїктесі

F) 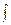signxdx=|x|+c

Егер берілсе, онда:

B)

D) оныѕ нїктедегі жанамасы

H) оныѕ нїктедегі жанамасыныѕ бўрыштыќ коэффициенті

Егер 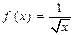берілсе, онда:

A)

C) оныѕ нїктесінде туындысы жоќ

D)

Егер функциясы берілсе, онда:

A) ол нїктесінде ґседі

B) аралыєында ол дґѕес (график дґѕестігі жоєары баєытталєан)

H) - оныѕ иілу нїктесі

Егер берілсе, онда:

//

ол аралыєында їзіліссіз функция.

Егер берілсе, онда:

// -їзіліс нїктесі

Егер берілсе, онда:

нїктеде функция аныќталмаєан//

//

Егер 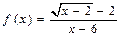берілсе, онда:

D) 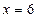нїктесінде аныќталмаєан

E)

F) Аныќталу аймаєы

Егер функциясы берілсе, онда:

A) оныѕ вертикаль асимптотасы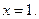

F) оныѕ кґлбеу асимптотасы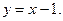

H) аралыєында ол ґседі

Егер функциясы берілсе, онда:

B) асимптотасы y=2, тїзуі

C) аралыєында ґседі

H) оныѕ еѕ кіші мјні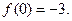

Егер функциясы берілсе, онда:

A) ол аралыєында ґседі

D) (-2;+ ) аралыєында функция ойыс (дґѕестігі тґмен баєытталєан)

F) функцияныѕ асимптотасы жоќ

Егер берілсе, онда:

B) аралыєында фунция ґседі

C) вертикаль асимптота жоќ

E) (1;+ )аралыєында функция ойыс (график дґѕестігі тґмен ќараєан)

Егер берілсе, онда:

F)

G) таќ функция

H)

Егер берілсе, онда:

A)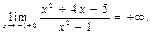

D)

G) жўп функция

Егер берілсе, онда:

B) нїктелерде функция їзіліссіз

E) - функцияныѕ 2 - текті їзіліс нїктесі

H) - функцияныѕ 2 - текті їзіліс нїктесі

Егер берілсе, онда:

E) - функцияныѕ 2 - текті їзіліс нїктесі

F) - функцияныѕ 2 - текті їзіліс нїктесі

H) жўп функция

Егер берілсе, онда:

D) 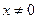нїктелерінде функция їзіліссіз

E)

H) - функцияныѕ 2 - текті їзіліс нїктесі

Егер шектері бар болса, онда:

C) шегі бар

D) -шенелген тізбек

H)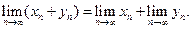

Егер берілсе, онда:

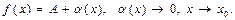
Егер шектері бар болса, онда:

A) шегі бар

D) -шенелген тізбек

F)

Егер 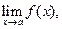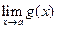шектері бар жјне олар аќырлы болса, онда:

A) шегі де бар

D)

H) функциясы нїктесініѕ маѕайында шенелген

Егер 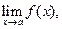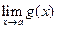шектері бар жјне олар аќырлы болса, онда:

A) шегі де бар

D)

H) функциясы нїктесініѕ маѕайында шенелген

Егер m саны сандыќ тізбектіѕ тґменгі шегі болса, онда:

A)

E)

G)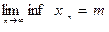

Егер M саны сандыќ тізбектіѕ жоєарєы шегі болса, онда:

C)

E)

G)

Егер жјне функцияларыныѕ нїктеде туындылары бар болса, онда:

А ) (u+х)ґ=uґ+хґ

E)

G)

Егер жјне функцияларыныѕ нїктеде туындылары бар болса, онда:

B)

E)

F)

Егер функцияларыныѕ нїктесінде n ретке дейінгі туындылары бар болса, онда:

C)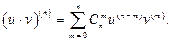

D)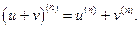

F) тўраќты

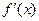Егер функциясы ќандай да бір аралыєында, ал ќандай да бір нїктесінде дифференциалданса, онда:

B) ƒ"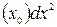

G) функция аралыєында їзіліссіз

H)

Дата добавления: 2015-10-24