Возражение третье

Третье возражение начинается с заявления, что (в рамках Байсовой логики) выборка в один элемент слишком мала, чтобы произвести значительные изменения в чьих-то рациональных убеждениях.

«основная идея… весьма проста: выборка размером в единицу катастрофически мала. То есть, каково бы свидетельство из этой выборки не было, априорное распределение размеров популяции будет доминировать в окончательном результате вычислений. Единственный путь избежать этой проблемы – это ввести узкие искусственный ограничения в пространство гипотез». (p. 406)

Затем они отмечают, что в пространстве гипотез, содержащем только две гипотезы, всё-таки может произойти существенный сдвиг:

«Если мы рассмотрим случай с двумя вариантами, описанный Бостромом, мы легко можем убедиться, что он прав насчёт вероятностей». (p. 406)

(Вероятность в этом примере сдвинулась с 50% до 99.999%, что наверняка «значительно», и подобный результат получается для широкого разброса изначальных вероятностей.) Но Корб и Оливер полагают, что такой значительный сдвиг может произойти только в том случае, если мы введём «узкие искусственный ограничения в пространство гипотез» путём рассмотрения только двух соперничающих гипотез вместе много большего их числа.

Легко убедиться, в том, что это неверно. Пусть {h1, h2, …hN} – пространство гипотез и путь Р – некая вероятностная функция, которая приписывает ненулевую вероятность всем этим гипотезам. Пусть hi будет наименее вероятной из этих гипотез. Путь e = исход одного случайного наблюдения. Не трудно убедиться, просто путём анализа формулы Байеса, что постериорная вероятность P(hi | e) может быть сделана произвольно большой путём выбора соответствующего e:

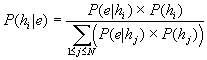
выбирая e так, чтобы P(e | hj) было малым для всех i не равно j, мы имеем:

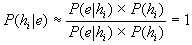
И действительно, мы получаем P(hi | e) = 1, если мы выбираем е таким P(e | hj) = 0, при i не равно j. (Это может соответствовать тому случаю, когда вы обнаруживаете, что ваш номер рождения 200 миллиардов, и тут же приписываете нулевую вероятность всем гипотезам, согласно которым людей меньше, чем 200 миллиардов)

Вывод: Оливер и Корб неправы, когда они заявляют, что изначальные данные всегда будут доминировать над любыми вычислениями, базирующимися на одном свидетельстве.

Дата добавления: 2015-10-24