Читайте также:
|
1°. Если хотя бы один элемент бесконечного произведения равен нулю, то бесконечное произведение расходится к нулю.
2°. На сходимость бесконечного произведения не влияет удаление(добавление) конечного числа множителей, если среди них нет равных нулю.
Теорема (критерий сходимости бесконечного произведения).
.Пусть (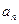
) – произвольная числовая последовательность и 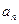> 0 при любом 
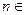N.
Бесконечное произведение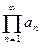 
сходится тогда и только тогда, когда сходится числовой ряд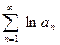 
Доказательство. См [ Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Продолжение курса. Под ред. А.Н.Тихонова. - М.: Изд-во МГУ, 1987. - 358 с.] c.47-48.
Дата добавления: 2015-09-04; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Бесконечные произведения | | | Двойные и повторные ряды |