Бесконечные произведения

К понятию числового ряда близко понятие бесконечного произведения.

Пусть (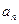) – произвольная числовая последовательность, вообще говоря комплексная.

Определение. Формальное б е с к о н е ч н о е произведение вида

называется бесконечным числовым произведением (или просто бесконечным произведением).

Обозначается 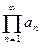или .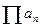

Определение. 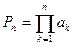называют n - ым частичным произведением

бесконечного произведения .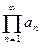

Определение. Если последовательность () частичных произведений имеет конечный предел, т.е существует ,

то бесконечное произведение 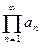называется сходящимся (к числу P ).

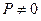Число P называется значением этого произведения.

Если P = 0, то бесконечное произведение 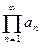называется расходящимся к нулю.

Если P = + ¥, то бесконечное произведение 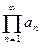называется расходящимся к плюс бесконечности.

Если предел не существует, то бесконечное произведение 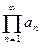называется расходящимся.

Пример 1. Бесконечное произведение 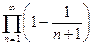расходится к нулю.

Решение. 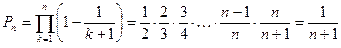. при .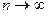

Пример 2. Бесконечное произведение 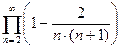сходится к .

Решение.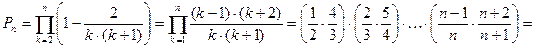

.

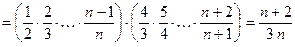Пример 3. Бесконечное произведение 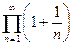расходится к плюс бесконечности.

Решение. . 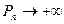при .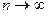

Теорема (необходимое условие 1 сходимости бесконечного произведения).

Если бесконечное произведение 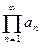сходится, то .

Доказательство. Так как , то .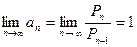

Важно! Начиная с некоторого номера сомножители бесконечного произведения не меняют знак, так как

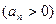при .

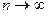Теорема (необходимое условие 2 сходимости бесконечного произведения).

Если бесконечное произведение 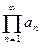сходится, то при .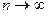

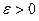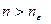Доказательство. Так как , по определению предела для любого найдётся номер такой, что при всех выполняется неравенство

,

,

,

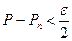откуда следует, что при .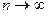

Дата добавления: 2015-09-04