Двойные и повторные ряды

Определение. Числовая функция 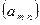двух натуральных аргументов ( 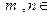N) называется двойной последовательностью.

Определение. Двойным рядом называется формальная б е с к о н е ч н а я сумма вида

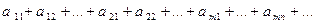
Обозначается 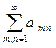или .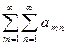

Определение. Конечная двойная сумма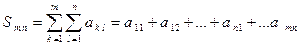

называется прямоугольной частичной суммой двойного ряда .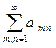

Определение. Конечный двойной предел S прямоугольной частичной суммы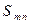

называется суммой двойного ряда .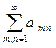

Напомним, что число S называется двойным пределом последовательности ,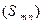

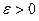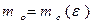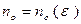если для любого найдутся номера и такие, что для всех пар (m, n) c условием 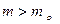и 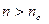выполняется неравенство

.

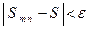Это определение полностью согласуется с общим определением предела функции по базе. В нашем случае база представляет собой совокупность окончаний 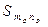, каждое из которых образовано множеством пар (m, n) c условием 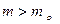и .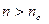

Для самой базы используют обозначение .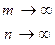

Для двойных пределов выполняются все свойства предела по базе. В частности, предел суммы равен сумме пределов. Имеет место единственность предела.

Теорема (необходимое условие сходимости двойного ряда).

Если двойной ряд 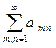сходится, то .

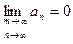Доказательство.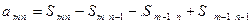

Теорема (критерий Коши сходимости двойного ряда).

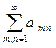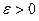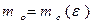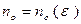Двойной ряд сходится тогда и только тогда, когда для любого найдутся номера и такие, что для всех пар (m, n) c условием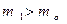 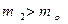и 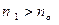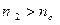выполняется неравенство

.

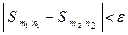Доказательство.

Теорема (критерий сходимости знакоположительного двойного ряда).

Двойной знакоположительный ряд 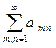сходится тогда и только тогда, когда

последовательность 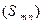прямоугольных частичных сумм этого ряда ограничена.

Доказательство. См [ Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Продолжение курса. Под ред. А.Н.Тихонова. - М.: Изд-во МГУ, 1987. - 358 с.] c.63.

Определение. Ряды 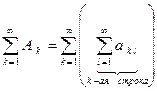и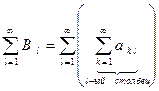

называются повторными.

Если убрать скобки можно получить двойной ряд 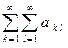. Надо оговаривать смысл. Вообще

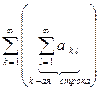¹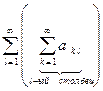

Пример 1. Рассмотрим матрицу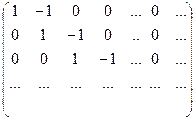

Ряд 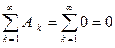и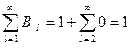

Суммы повторных рядов не равны.

Определение. Повторный ряд 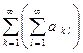называется сходящимся, если при любом k Î N ряд 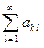сходится к числу 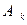и ряд 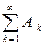сходится к числу S.

В этом случае число S называется суммой повторного ряда .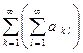

Повторный ряд 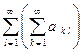называется сходящимся, если при любом l Î N ряд 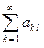сходится к числу 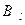и ряд 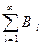сходится к числу S.

В этом случае число S называется суммой повторного ряда .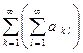

Дата добавления: 2015-09-04