Пример работы с динамическими уравнениями цепи.

К цепи, состоящей из последовательного соединения резистора R и индуктивности L, прикладывается напряжение, график которого пред-ставлен на рисунке. Полагая, что i(0_) = 0, найти закон изменения тока в цепи в функции времени.

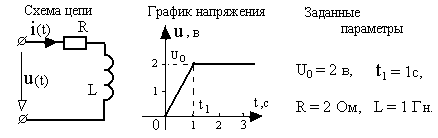Решение.

1. Записываем заданное напряжение в аналитической форме, после чего описываем цепь уравнением по II закону Кирхгофа:

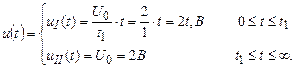
Цепь описывается всего одним уравнением по II закону Кирхгофа:

или по каждому из интервалов:

2.Решение этих диффуравнений будем находить в виде суммы принуждённой и свободной составляющих:

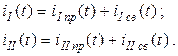
3.Принуждённые составляющие будут вид, соответствующий виду правой части уравнений

Коэффициенты a _I, b _I, a _II найдём подстановкой частных решений в исходные дифференциальные уравнения:

Приравнивая коэффициенты при переменных, получаем:

a _I =2/R = 1; b _I= - L a _I /R = - 0.5; a _II = U₀/R = 1.

4.Свободные составляющие, как общее решение уравнения с нулевой правой частью, записываем в виде экспонент:

Постоянные интегрирования А₁, А₁₁ находим из начальных усло-вий, которые подставим в полные решения диффуравнений по интервалам:

При t = 0 ток в индуктивности и тогда постоянная интегрирования A_I = +0.5.

Постоянную интегрирования А_II найдём из условия, записанного на основании первого закона коммутации для цепи с индуктивностью в момент t₁ :

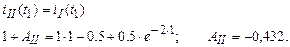
5. Окончательное выражение тока цепи по интервалам будет:

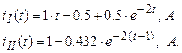
По полученным выражениям строим график тока.

Чтобы построить также графики мощности и энергии в элементах цепи, необходимо получить их выражения конкретно для рассматриваемой цепи.

Предлагается выполнить это самостоятельно. Напомним, что мгновенная мощность в L и С элементах может иметь знак минус. Это означает, что в данный момент энергия, запасённая в этих элементах, отдаётся источнику.

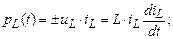
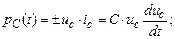
В данном примере изложен общий подход к решению динамических уравнений цепи: задано напряжение на входе всей цепи и параметры элементов.

Иногда, если заданы ток или напряжение на одном из элементов, расчёт можно выполнить проще, воспользовавшись известными соотношениями между током и напряжением каждого элемента. Рассмотрим такой пример.

Пример упрощённого расчёта ЛИВ цепи

Требуется найти законы изменения напряжений на резисторе u _R 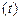, на индуктивности u _L 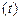и на источнике тока , получить выражения и построить графики мощностей элементов и цепи в целом.

РЕШЕНИЕ

1.Заданный графически ток источника записываем в аналитической форме:

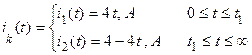
2. Напряжение на резисторе находим по закону Ома, а на индуктивности – по закону электромагнитной индукции:

Напряжение на источнике тока находим по II закону Кирхгофа:

3. Мгновенные мощности элементов равны произведениям напряжения на элементе на ток в элементе. Полные выражения мгновенных напряжений

и мощностей на элементах цепи приведены непосредственно на графиках.

* Переработано для студентов потока ТКС. АВХ, 10августа 2002г.

------------------ххх-------------------

Дата добавления: 2015-09-04