Классическая опред. Вероятности

Предполагает т/ко конечное мн-во всех элем.событий,причем все соб-я должны быть равновозможными.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой P(A) = m/n, где m-число элементарных исходов, благоприятствующих А; n-число всех возможных элементарных исходов испытания. Здесь предполагается, что элементарные исходы не совместны, равновозможные и образуют полную группу. Из определения вероятности вытекает следующие свойства: 1.Вероятность достоверного события равна единице. 2.Вероятность невозможного события равна нулю. 3.Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0 <m/n<1, следовательно, 0<P(A)<1. Итак, вероятность любого события удовлетворяет двойному неравенству 0 <= P(A)<= 1.

3.Геометрическая вероятность Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности -вероятность попадания точки в область(отрезок, часть плоскости и т.д.). Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P= Длинаl/длинаL

5.Вероятность суммы событий. Суммой событий A и B наз-ся событие, при котором произошло или A, или B, обозначается оно A + B.Вчастности, если 2-а события А и В несовместные

то А + В - событие, состоящее в появлении одного из этих событии, безразлично какого. Теорема сложения вероятностей Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Р(А)+Р(В)=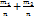

6.Вероятность произведения событий Произведением двух событий А и В наз-ют соб.АВ,состоящее в совместном появлении

этих событий,т.е и А и В.

Условная вероятностью 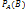называют вероятность соб.В,вычисленную в пред-положении,что соб.А уже наступило.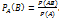

Событие А наз-ся зависимым от события В вероятность наступления события A зависит от того, наступило событие B или нет.

Соответственно, для зависимых событий p (AB) = p (B) p (A / B).

Независимыми называются события A и B, если вероятность события A не зависит от того, наступило событие B или нет.,т.е Условн.вероят.соб.В = его безусловной вероят:

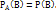Два события наз-ют независимым,если вероят-ть их совмещения =произвед-ию вероятн-ей этих событий. P(AB)=P(A)∙P(B)

Т:умнож.вероятн-ей:Вероят-сть появления 2-ух завис. событий равна произв-ию вероят-тей одного из них на вероятность др-го вычисленную при условии, что 1-ое событие уже наступило. Р(АВ)=Р(А)∙ 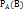; P(BA)=P(B)∙ .

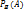Вероят-ть произвед. неск-их событий равна произвед-ю вероят-ей этих событий причем вероят-ть каждого next события вычисляется при условии, что все предыдущие уже наступили. P(ABC)=P(A)∙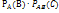

Вероят-ть появления хотя бы1-ого события А1,А2..,Аn,независимых в совокуп-ти,равна разности м/у 1 и произведением вероятностей противопол-х событий 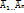: Р(А)=1-q1∙q2..qn;

ЧС:если соб. А1,А2..,Аn,имеют одинаковую вероят-ть=р,то верот-ть появления хотя бы 1-ого из этих событий Р(А)=1- .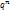

7.Формула полной вероятности Вероятность появления соб.А,которое может наступить лишь при условии появление одного из несовместных соб-ий В1,В2..Вn,образующих полную группу,равна сумме произвед-ий вероятностей каждого из этих событий на соответствующую условную вероят-ть А:

1) +..

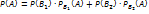Событие А может произойти только вместе с каким-либо из событий В1,В2..Вn, которые будем называть гипотезами

8.Формула Бейса Пусть имеется полная группа попарно несовместных гипотез В1,В2..Вn с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло

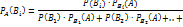
9.Формула Бернулли (повтор.испытаний). Если производится нес-ко испытаний, причем вероятность соб. А в каждом испытании не зависит от исходов других испытаний, то такие испытания наз-ют "независимыми относительно соб.А" (Соб. А имеет одну и ту же вероятность), (одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других.)"Сложное событие"- совмещение нескольких отдельных событий, которые наз-ют "простыми". Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Теорема. Если производится n независимых опытов в каждом из которых событие А появляется с одинаковой вероятностью р,то тогда вероятность того, что соб. А появится ровно m раз опред-ся по формуле. Где q=1-р

;

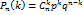
Формула Бернули позволяет вычислить вероят-ть того,что соб.появится в n испытаниях k раз.

-.Дискретная случайная величина. Функция распределения Опытом называется всякое осуществление определенных условий и действий при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать качественно и количественно. Случайной называется величина, которая в результате опыта может принимать то или иное значение., причем заранее не известно какое именно. Случайные величины принято обозначать (X,Y,Z), а соответствующие им значения (x,y,z)

Случайная величина наз-ся числовая переменная величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями. случайная величина определяет вероятность m успехов в n испытаниях.

Дискретной называется случайная величина, которая при испытаниях может принимать одно из изолированных значений, количество которых конечно. Непрерывной называют случайную величину, которая может принимать все значения из некоторого (бес)конечного промежутка. Законом распределения случайной величины называется соответствие между возможными значениями случайных величин и их вероятностями

9.Числовые характеристики дискретных случайных величин Модой (Мо) случайной величины х называется наиболее вероятное ее значение. Это определение строго относится к дискретным случайным величинам. Для непрерывной величины модой называется такое ее значение для которого ф-ция плотности распределения имеет максимальную величину. Медианой (Ме) случайной величины называется такое ее значение для которого окажется ли случайная величина меньше этого значения. Для непрерывной случайной величины медиана это абсцисса точки в которой площадь под кривой распределяется пополам. Для дискретной случайной величины значение медианы зависит от того четное или нечетное значение случайной величины n=2k+1, то Ме=х_к+1 (среднее по порядку значение) Если значение случайных величин четное, т.е n=2k, то

Дата добавления: 2015-09-02