Равномерное распределение

Закон равномерного распределения вероятностей непрерывной случайной величины используется при имитационном моделировании сложных систем на ЭВМ как первоначальная основа для получения всех необходимых статистических моделей. При этом, если специально не оговорен закон распределения случайных чисел, то имеют ввиду равномерное распределение. Распределение вероятностей называют равномерным, если на интервале (a,b), которому принадлежат все возможные значения случайной величины, дифференциальная функция распределения имеет постоянное значение, т. е. f(x) = C. Так как то Отсюда закон равномерного распределения аналитически можно записать так: 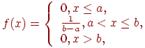График дифференциальной функции равномерного распределения вероятностей представлен на рис.

12.Биномиальное распределение. Биномиальное распределение вероятности описывает процессы, в каждом из которых событие A может появиться с вероятностью p. Тогда вероятность того, что событие A наступит ровно k раз, определяется формулой.

При биномиальном распределении дисперсия равна мат. Ожиданию умноженному на вероятность появления события в отдельном опыте.

?. Распределение Пуассона Закон Пуассона действует всякий раз, когда имеется много независимых испытаний N, а вероятность p каждого испытания так мала, что среднее число событий λ = pn с данным исходом невелико.

Л=np

n-число проведенных опытов

р-вероятность появления события в каждом опыте

В теории массового обслуживания параметр пуассоновского распределения определяется по формуле

а=λt, где λ - интенсивность потока сообщений t-время

Необходимо отметить, что пуассоновское распределение является предельным случаем биномиального, когда испытаний стремится к бесконечности, а вероятность появления события в каждом опыте стремится к 0. Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.

10-11. Локальная и интегральная теорема Лапласа Если число опытов достаточно велико,но не бесконечно, а вероятность появления события А в каждом опыте не стремится к 0, применяют локальную и интегральную Т: Лапласа Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р причем 1>р>0, то это событие наступает ровно m раз приблизительно равна

Интегральная теорема Лапласа. Пусть проводится n независимых испытаний, причем вероятность появления события p постоянна и отлична от нуля и от единицы, то вероятность того, что в n испытаниях событие наступит от k 1 до k 2 раз приблизительно

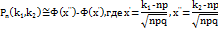
Дата добавления: 2015-09-02