а) Дисперсия

Отклонение-это разность м/у случайной величиной и её мат.ожиданием

Отклонение значений: Х-М(Х)∙p +х₁-М(Х) ∙p +х₂-М(Х)∙p₃

Среднее значение отклонения от мат.ожидания: М[X-M(X)]=0

Дисперсией случайной дискретной величины называется среднее значение квадрата отклонения случайной величины от её матем.ожидания: D(X)=M[X-M(X)]²⁼

Квадрат отклонения: [х₁-М(Х)]² ∙p₁ +[х₂-М(Х)]²∙p_2..

Формула для вычисления:D(X)=M(X²)-[M(X)]², М(Х)=∑Xp

Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю: D(С) = 0
2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х)
3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ±... ± Х_n) = D(Х₁) + D(Х₂) +... + D(Х_n)

Среднее квадратическое отклонение случайной величины Х наз-ют квадратный корень из дисперсии: σ(X) = √D(X)

- Биномиальный закон ( распределение Бернулли)

M(Х)=np; D[X]=npq

-Характерной особенностью распределения Пуассона являются совпадения математического ожидания и дисперсии, причём:M(Х)=D[X]=Л

- Геометрический закон распределения:

M(Х)=1/p; D[X]=q/p²

- Равномерное распределения: M(Х)= 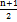; D[X]=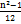

Дата добавления: 2015-09-02