Вероятностей. В процессе эксплуатации эффективность функционирования ЭВМ можно оценивать по числу

В процессе эксплуатации эффективность функционирования ЭВМ можно оценивать по числу отказов определенного типа, по времени, прошедшему от момента отказа до окончания ремонта, по времени от момента окончания ремонта до момента следующего отказа и т.д. Т.е. для описания процесса эксплуатации можно использовать случайные величины различного рода: дискретные (такие как число отказов) и непрерывные (такие как длительность восстановления или время между отказами). Случайная величина описывается соотношениями между значениями случайной величины и вероятностями их появления. Эти соотношения задаются законом распределения случайной величины.

Так, задать закон распределения дискретной случайной величины Х означает перечислить все ее возможные значения x₁, x₂... и соответствующие им вероятности появления P₁, P₂...

Для количественной характеристики распределения вероятностей удобно воспользоваться не вероятностью для Х=х, а вероятностью для Х<х, где х – некоторая текущая переменная. Вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, называется функцией распределения случайной величины Х и обозначается F(x): F(x)=P(X<x). Её также называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин (прерывных и непрерывных), т.е. является одной из форм закона распределения.

Рассмотрим свойства функции распределения.

1. при х₂>х₁ имеем F(x₂)³F(x₁) т.е это неубывающая функция своего аргумента;

2. F(–¥)=0;

3. F(+¥)=1;

Графически F(x) можно представить в следующем виде:

Зная ряд распределения прерывной случайной величины, можно легко построить функцию распределения:

где x_i<x под знаком суммы указывает, что суммирование распространяется на все те значения x_i, которые меньше х. Когда текущая переменная х проходит через какое-нибудь из возможных значений случайной величины Х, то функция распределения меняется скачкообразно, причём величина скачка равна вероятности этого значения.

Рассмотрим следующее понятие – плотность распределения. Пусть имеется случайная величина Х с функцией распределения F(x), непрерывной и дифференцируемой. Вычислим вероятность попадания случайной величины на участок от х до х+Dх:

P(x<X<x+Dх)=F(x+Dх)–F(x)

т.е. мы имеем приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке. Будем приближать Dх к нулю. В пределе получим производную от функции распределения:

Введём обозначение f(x)=F¢(x). Функция f(x) – производная от F(x) – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке.

Эта функция называется плотностью распределения (т.е. плотностью вероятности) непрерывной случайной величины Х. Иногда её называют дифференциальной функцией распределения. Плотность распределения, также как и функция распределения, является одной из форм закона распределения. Но в отличие от функции распределения – плотность распределения не является универсальной функцией – она существует только для непрерывных случайных величин. Свойства плотности распределения:

¨ плотность распределения – это неотрицательная функция: f(x)³0 (т.е. кривая распределения лежит не ниже оси абсцисс).

Это свойство вытекает из того, что функция распределения F(x) есть неубывающая функция;

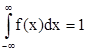(т.е. геометрически, полная площадь под кривой распределения равна единице).

Иногда для определения вероятностных характеристик процесса эксплуатации ЭВМ необходимо отыскивать закон распределения функции случайных величин, например закон распределения суммы двух независимых случайных величин Х и Y. Если плотности распределения случайных величин Х и Y соответственно , то плотность распределения 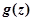случайной величины может быть определена по одной из формул

Генеральной совокупностью называется все множество значений, которые может принять случайная величина из области определения.

Генеральная совокупность значений случайной величины кроме закона распределения характеризуется рядом числовых величин, таких как момент s-го порядка.

Моменты бывают начальные и центральные. Они описывают то или иное свойство распределения. Начальным моментом S-го порядка (а именно такими величинами являются времена между отказами и времена восстановления) дискретной случайной величины Х называется сумма вида:

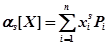
Для непрерывной случайной величины:

Очевидно, что мат. ожидание – это первый начальный момент (S=1).

Центрирование случайной величины равносильно переносу начала координат в среднюю «центральную» точку, абсцисса которой равна мат. ожиданию:

Моменты центрированной случайной величины носят название центральных моментов. Центральным моментом порядка S случайной величины Х называется мат. ожидание S-й степени соответствующей центрированной случайной величины:

Для дискретной случайной величины:

Для непрерывной случайной величины:

Наиболее часто применяют 1-й начальный момент (мат. ожидание) a₁ и 2-й центральный момент (m₂ – дисперсия).

Согласно определению центрального момента . Дисперсией случайной величины Х называется мат. ожидание квадрата соответствующей центрированной величины, или

Для дискретной случайной величины:

Для непрерывной случайной величины:

Дисперсия случайной величины – это характеристика рассеивания, т.е. разбросанности значений случайной величины около её мат. ожидания. Дисперсия случайной величины имеет размерность квадрата случайной величины.

Среднее квадратическое отклонение (СКО) .

Безразмерный коэффициент вариации, определяемый как отношение среднего квадратического отклонения к математическому ожиданию, численно определяет степень отклонения случайной величины от математического ожидания.

Следует отметить, что мат. ожидание m_x и дисперсия D_x – наиболее часто применяемые характеристики случайной величины. Они характеризуют соответственно положение и степень разбросанности.

Третий центральный момент m₃ служит для характеристики асимметрии (или «скошенности») распределения. Коэффициент асимметрии: S_x=m₃/s³. Для симметричных распределений S_x=0. Если S_x>0, то асимметрия правосторонняя, т.е. правый «хвост» распределения длиннее левого. Если S_x<0, то наоборот, асимметрия левосторонняя.

Четвёртый центральный момент m ₄ служит для характеристики крутости (т.е. островершинности) распределения. Эксцесс или крутость распределения случайной величины Х – это безразмерное число:

Число 3 вычитается для того, чтобы подчеркнуть отличие от нормального распределения, для которого m₄/s⁴=3. Принято, что для нормального распределения . Кривые, более островершинные, по сравнению с нормальным распределением, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом.

Рассмотрим законы распределения случайных величин, наиболее широко используемые в теории эксплуатации ЭВМ.

Для описания дискретных случайных величин используются следующие законы распределения:

1. Дискретное пуассоновское распределение с параметром :

,

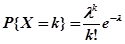где – целое число.

Для пуассоновского распределения математическое ожидание, дисперсия и центральный момент третьего порядка равны 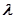, а коэффициент вариации равен 1/ .

2. Геометрическое распределение с параметром р:

, ,

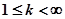где – целое число.

Математическое ожидание случайной величины X, имеющей геометрическое распределение, равно 1/р, дисперсия (1—р)/р2, коэффициент вариации .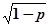

3. Биномиальное распределение. Оно применяется если дискретная случайная величина является усеченной, принимающей значения, например, в интервале и задаваетя выражением

где – целое число.

Математическое ожидание случайной величины, имеющей биномиальное распределение, равно пр, дисперсия nр(1—р), коэффициент вариации .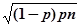

4. Дискретное равномерное распределение. Иногда используется для случайных величин, определенных на интервале ; в этом случае вероятность того, что случайная величина примет значение, равное , равно . Математическое ожидание такой случайной величины равно , дисперсия .

Рассмотрим законы распределения вероятностей, которые широко используются для описания непрерывных случайных величин.

1. Экспоненциальное распределение с плотностью

где 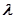– параметр распределения, связанный с математическим ожиданием и дисперсией выражениями

и .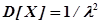

Особенностью экспоненциального распределения является то, что коэффициент вариации этого распределения равен 1.

Рис. Экспоненциальное распределение ()

2. Распределение Эрланга k-го порядка с плотностью

где – целое число, а параметр 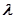связан с математическим ожиданием выражением:

.

Легко заметить, что при k=1 имеем экспоненциальное распределение.

Можно показать, что случайная величина, имеющая эрланговское распределение, может рассматриваться как сумма k случайных величин, имеющих экспоненциальное распределение с параметром 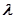. Другими словами, если в потоке событий длительность интервалов между моментами возникновения событий будет иметь эрланговское распределение, то такой поток событий можно рассматривать как поток, полученный путем регулярного прореживания пуассоновского потока (удаления подряд следующих событий).

Эрланговское распределение времени между событиями при 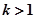характеризуется меньшей дисперсией, чем при экспоненциальном распределении. Его дисперсия

.

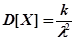Рис. Распределения Эрланга

2-го и 3-го порядка ()

3. Гамма-распределение с параметрами и 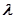, определяемое плотностью

, ,

где – гамма-функция; а>0 – параметр формы.

Математическое ожидание случайной величины, имеющей гамма-распределение, определяется формулой

,

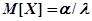а дисперсия

.

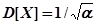При целых гамма-распределение совпадает со специальным распределением Эрланга.

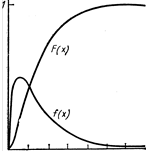
Рис. Гамма-распределение ().

4. Распределение Вейбулла с параметрами и 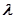, определяемое плотностью

где а>0 — параметр формы распределения.

Математическое ожидание в этом случае определяется выражением

,

дисперсия

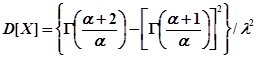
Функция распределения для закона Вейбулла записывается в виде

,

откуда следует, что распределение Вейбулла может быть получено из экспоненциального распределения путем степенного преобразования масштаба времени.

Рис. Распределение Вейбулла ()

5. Нормальное распределение, определяемое плотностью

,

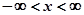где т=М[Х] – первый параметр распределения; – среднее квадратическое отклонение.

6. Логарифмически-нормальное распределение

,

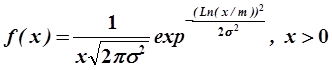где m>0 – параметр формы, связанный с математическим ожиданием случайной величины х соотношением

М[Х]=Ln т

Дисперсия логарифмически-нормального распределения

,

где

Рис. Логарифмически-нормальное

распределение

Остановимся дополнительно на экспоненциальном распределении, играющем исключительно важную роль в теории эксплуатации ЭВМ, так как это распределение связано с таким важным понятием, как пуассоновский поток событий.

Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени.

Пуассоновский поток событий — поток, для которого длительность интервалов между событиями является случайной величиной, имеющей экспоненциальное распределение, задаваемое выражением 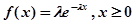, в котором параметр l интерпретируется как интенсивность потока событий.

Важное свойство пуассоновского потока событий заключается в том, что вероятность появления нового события в течение интервала времени 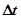определяется только длиной интервала 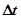и интенсивностью потока событий 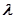, но не зависит от предыстории, т. е. от того, сколько и когда произошло событий в прошлом. Таким образом, для пуассоновского потока характерно отсутствие последействия. Промежутки времени между моментами наступления событий в пуассоновском потоке – независимые случайные величины, а вероятность того, что за время [0,t] наступит точно k событий, определяется выражением

Другими словами, дискретная случайная величина (число наступивших событий, например число отказов ЭВМ в течение интервала времени t ,) определяется дискретным распределением Пуассона с параметром 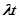(математическим ожиданием числа отказов, равным 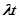). Данное свойство характеризует пуассоновский поток как стационарный. Отметим следующие свойства пуассоновского потока.

I. Пуассоновский поток ординарен – вероятность двух событий и более в момент времени t практически равна нулю.

II. При случайном прореживании пуассоновского потока с интенсивностью 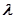, когда с вероятностью наступившее событие оставляется, а с вероятностью отбрасывается, получается пуассоновский поток с интенсивностью .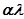

III. При наложении независимых пуассоновских потоков с интенсивностями 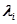; , и образуется пуассоновский поток с суммарной интенсивностью .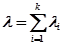

IV. Остаток времени от случайно взятой точки до ближайшего события в пуассоновском потоке с интенсивностью 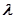есть случайная величина, имеющая экспоненциальное распределение с тем же параметром .

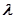Дата добавления: 2015-09-02