Модели потоков восстановления

Большинство ЭВМ являются восстанавливаемыми системами. Время восстановления 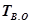работоспособного состояния ЭВМ после наступления устойчивого отказа – величина случайная, характеризуемая функцией распределения

(2)

или плотностью распределения

По аналогии с интенсивностью отказов 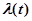вводится интенсивность восстановления –условная плотность распределения вероятностей времени до восстановления ЭВМ при условии, что до момента времени 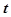работоспособность ЭВМ восстановлена не была.

В ряде случаев время восстановления (суммарное время работы обслуживающего персонала по поиску неисправности, замене отказавшего элемента и проверке работоспособности с помощью специальных тестов) можно считать случайной величиной, имеющей экспоненциальное распределение с постоянной интенсивностью , тогда

.

В этом случае среднее время восстановления

,

т. е. интенсивность восстановления – величина, обратная математическому ожиданию времени восстановления.

При появлении отказа в ЭВМ невозможна мгновенная замена отказавшего элемента, так как время поиска и замены ТЭЗ (не говоря уже о замене логического элемента в ТЭЗ) случайно или отлично от нуля.

В самом простейшем случае, когда численность обслуживающего персонала такова, что поиск неисправности и ее устранение начинаются практически сразу после ее возникновения, основной характеристикой восстановления ЭВМ является вероятность того, что работоспособность ЭВМ будет восстановлена за заданное время 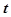эта вероятность определяется по (2).

Случайная величина 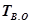представляет собой, как отмечалось ранее, сумму двух случайных величин: времени поиска причины отказа и времени его устранения (замены ТЭЗ) с учетом времени проверки работоспособности ЭВМ после ремонта :

.

Функция плотности распределения 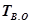может быть найдена по формуле композиции законов распределения (2.14):

,

где – плотности распределения времен поиска и устранения отказа.

Если предположить, что 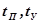– случайные величины, имеющие экспоненциальные распределения с одним и тем же параметром , то

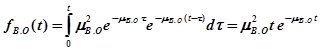. (3)

Как следует из данной формулы, время восстановления имеет эрланговское распределение второго порядка. Данный факт имеет достаточно простую физическую интерпретацию: в силу сложности устройств ЭВМ вероятность восстановления ЭВМ за очень малое время практически равна нулю. Практически равна нулю и вероятность длительной работы по восстановлению, так как современные ЭВМ снабжаются развитой системой диагностики и комплектации.

Функция распределения времени восстановления при , определенной (3), имеет вид

,

причем | – интенсивность восстановления; 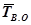– среднее время восстановления.

Рассмотрим, каким образом может быть определен коэффициент готовности ЭВМ с учетом интенсивностей потока отказов и восстановлений. Сделаем предположение о том, что длительность интервалов работы ЭВМ между моментами появления отказов есть случайная величина, имеющая экспоненциальное распределение с параметром 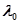, а длительность восстановления – экспоненциально распределенная случайная величина с параметром . Будем считать, что ремонт (устранение отказа) начинается сразу после наступления отказа (это можно интерпретировать так: время поиска включено во время ремонта). После окончания ремонта ЭВМ сразу приступает к выполнению заданий.

Таким образом, ЭВМ может находиться в двух состояниях: работоспособном и неработоспособном, когда проводится восстановление. Обозначим эти состояния соответственно символами и .

Пусть вероятности нахождения ЭВМ в состояниях и обозначены как и . Если ЭВМ исправна в момент времени , то .

Для определения аналитической зависимости и от времени вычислим вероятность того, что ЭВМ будет находиться в состоянии в момент времени , где 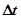– малый интервал времени.

Если в момент времени ЭВМ находилась в состоянии , то она в течение времени 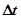останется в этом состоянии с вероятностью . Если в момент времени 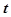ЭВМ находилась в состоянии , то за интервал времени 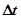она перейдет в состояние с вероятностью .

Таким образом, можно записать

.

С учетом того, что при малых 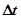, , имеем

.

Преобразовав это выражение, получим

,

что при дает следующее дифференциальное уравнение Колмогорова:

. (4)

Так как для любого момента времени 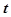выполняется равенство

, (5)

уравнение (4) может быть переписано в виде

.

Это уравнение описывает процесс эксплуатации ЭВМ, на функционирование которой оказывают влияние потоки отказов и восстановлений. Его аналитическое решение имеет следующий вид:

,

где .

Нетрудно заметить, что при полученное выражение стремится к пределу, равному – стационарной (установившейся) вероятности нахождения ЭВМ в состоянии :

.

Используя (5), получаем стационарную вероятность

.

Стационарная вероятность есть не что иное, как доля времени работоспособного состояния машины или, другими словами, коэффициент готовности. Действительно,

Восстановление после сбоев

Время восстановления после сбоя 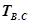складывается из времени идентификации ошибки как сбоя, времени фиксации сбоя (с целью накопления статистики о сбоях) и времени автоматического рестарта. Время восстановления после сбоя можно считать случайной величиной, задаваемой функцией распределения . Среднее время восстановления после сбоя в этом случае оценивается как математическое ожидание случайной величины 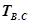, заданной функцией распределения .

Дата добавления: 2015-09-02