Модели потоков отказов и сбоев

Под аналитической моделью некоторого процесса понимают совокупность математических зависимостей, описывающих его протекание с подробностью и точностью, соответствующей решаемой задаче исследования процесса. Поведение ЭВМ при эксплуатации зависит от ряда случайных факторов, таких как возникновение отказов, сбоев, восстановление работоспособности машины.

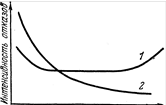
Рис.1. Зависимость интенсивности отказов от времени эксплуа тации аппаратурных (1) и программных (2) средств

Безотказность аппаратуры зависит от времени ее функционирования (кривая 1 на рис. 1). В начале периода функционирования на этапе обнаружения и исправления ошибок проектирования и производственных дефектов интенсивность отказов аппаратуры уменьшается со временем. Затем в течение большей части срока службы она остается примерно постоянной. Именно этот период эксплуатации представляет наибольший интерес. В конце срока службы интенсивность потока отказов значительно увеличивается вследствие износа аппаратуры. Особенности зависимости безотказности программных средств от времени (кривая 2 на рис. 1) обсудим позднее.

Рассмотрим основные характеристики потока отказов, базирующиеся на законе распределения интервала времени между отказами.

Основной характеристикой является вероятность безотказной работы ЭВМ 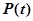– вероятность того, что ЭВМ сохранит работоспособность до момента времени 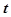. Если 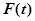– функция распределения времени безотказной работы ЭВМ 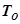, то вероятность безотказной работы 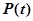– это функция, дополнительная к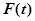

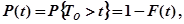
причем 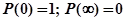, т.е. в момент начала эксплуатации с вероятностью 1 ЭВМ исправна, при завершении срока эксплуатации ЭВМ практически непригодна к использованию.

Функцию 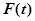в литературе по надежности часто называют вероятностью отказа, а также функцией ненадежности или функцией риска и обозначают :

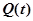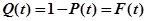
Используя функцию распределения 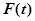, можно определить такой параметр, как среднее время безотказной работы:

,

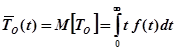где 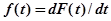– плотность распределения случайной величины .

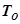С помощью 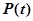можно оценить также и среднее число элементов (устройств) ЭВМ 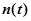, которые откажут за интервал времени :

,

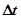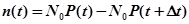где, 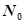– число исправных элементов (устройств) ЭВМ в начале ее эксплуатации.

Введем понятие интенсивности отказов 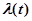как условную плотность распределения вероятностей времени до возникновения отказа при условии, что до момента времени 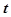отказа не было.

Таким образом, вероятность того, что первый отказ произойдет в интервале времени ,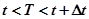

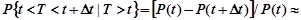
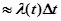
Аналогично

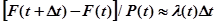
откуда

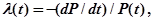(1)

или

.

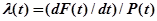Рассмотрим далее уравнение (1). Из него получаем

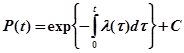
Постоянную С можно найти, воспользовавшись начальными условиями при 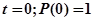, откуда .

Таким образом, вероятность безотказной работы связана с интенсивностью отказов 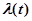выражением

,

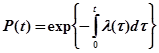или

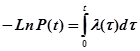
Если интенсивность отказов 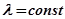, то можно показать, что

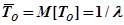
Другими словами, 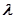– среднее число отказов в единицу времени.

Приведенные результаты еще раз подчеркивают важность экспоненциального распределения в теории эксплуатации ЭВМ, поскольку, как отмечалось выше, для основных режимов функционирования ЭВМ (исключая период первичной приработки и периоды физического износа уз лов и элементов) предположение 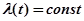практически выполняется.

ЭВМ состоит из большого числа отдельных устройств, таких как процессоры, каналы, внешние устройства и т. д. В свою очередь каждое из них (устройств) состоит из отдельных логических элементов. Их число в разных устройствах различно. Имеются различия в режимах работы отдельных устройств в целом. Это обусловливает неравномерность выхода из строя устройств ЭВМ: каждое устройство характеризуется своей интенсивностью отказов 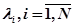, где 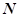– число типов устройств ЭВМ.

Если время безотказной работы 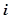-го устройства ЭВМ есть случайная величина, имеющая экспоненциальное распределение с параметром 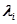, то вероятность его безотказной работы за время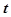

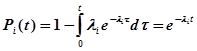(2)

Будем считать, что события – отказы устройств различного типа – независимы между собой, тогда вероятность безотказной работы ЭВМ

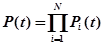
где 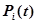– вероятность отказа устройства 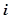-го типа за время 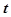; 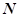– число устройств в составе ЭВМ.

На основании (2) получаем

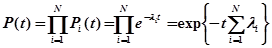
Нетрудно заметить, что эта формула отражает одно из свойств пуассоновского потока: при наложении нескольких пуассоновских потоков снова имеем пуассоновский поток с интенсивностью, равной сумме интенсивностей отдельных потоков.

Рассмотрим, как можно вычислить вероятность безотказной работы, если известна функция распределения времени наработки на отказ отдельных устройств ЭВМ. Очевидно, что если ЭВМ содержит N устройств, то для нерезервированной ЭВМ выход одного устройства из строя означает отказ ЭВМ в целом. Другими словами, если через 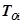обозначить случайную реализацию времени наработки на отказ 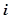-го устройства, то случайная реализация времени наработки на отказ ЭВМ в целом

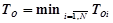
Так как 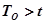только в том случае, если 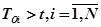, то вероятность безотказной работы ЭВМ

.

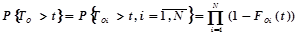Для упрощения можно считать, что надежность всех устройств ЭВМ одинакова; более того, так как время наработки на отказ одного устройства значительно больше времени наработки на отказ ЭВМ в целом, в первом приближении можно считать, что при малых t 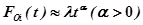. Тогда при достаточно больших N и одинаковых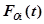

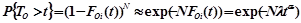
Введем в рассмотрение случайную величину 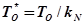, где – нормирующая константа, выбранная таким образом, чтобы 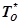имело предельное распределение при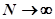

.

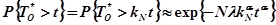Если положить 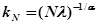, то будем иметь

.

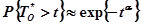Таким образом, нормированная величина 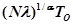в качестве предельного имеет распределение Вейбулла.

Полученные выражения позволяют оценить вероятность безотказной работы ЭВМ в течение заданного интервала времени.

Выше были рассмотрены простейшие модели потока отказов ЭВМ в предположении, что интервалы между моментами появления отказов являются одинаково распределенными случайными величинами.

Дата добавления: 2015-09-02