Приведение уравнения кривых второго порядка к каноническому виду

Если кривая задана уравнением

a11x2 + a22y2 + 2a12xy + a01x + a02y + a00 = 0, (7.21)

92 7. Приложение линейной алгебры

то это уравнение можно привести к каноническому виду путём пе- рехода к новой системе координат. Этот процесс можно разбить на два этапа.

1. Отыскание главных осей квадратичной формы

B = a11x2 + a22y2 + 2a12xy.

Для этого находим её собственные числа λ1 и λ2 и собственные векторы. Если окажется, что λ1 · λ2 > 0, то кривая эллиптического типа, если λ1 · λ2 < 0, то гиперболического типа. При λ1 · λ2 = 0 име- ем кривую параболического типа. Приняв в качестве новых базис- ных векторов декартовой системы главные оси квадратичной фор- мы, уравнение (7.21) приведём к виду

λ1x2 + λ2y2 + ax1 + by1 + c = 0,

1 1

причём (a, b) = (a01, a02)Q, где Q - матрица перехода от старого ортонормированного базиса к новому.

2. Отыскание нового начала системы координат O1, преобразова- ние параллельного переноса начала O в точку O1.

Как это делать практически, покажем на примере. Предполага- ем, что все системы координат имеют правую ориентацию.

Пример 1. Построить кривую

x2 + y2 + xy − 3x − 3y = −2. (а) Приводим квадратичную форму B = x2 + y2 + xy к главным осям

1 0,5

(как в п. 6.7). Её матрица B =

0,5 1.

Записываем характеристическое уравнение этой матрицы

Его корни λ1 = 0,5, λ2 = 1,5 являются собственными числами. Так как λ1 · λ2 > 0, то кривая (а) - эллипс. Координаты собственно- го вектора, отвечающего числу λ1 = 0,5, удовлетворяют соотноше- нию ξ1 + ξ2 = 0. В качестве нового базисного вектора примем вектор

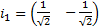. Другой базисный вектор . Записываем матрицу Q перехода от базиса 0,i,j к 0,i₁,j₁:

9.5. Эллипс. Гипербола. Парабола 147

В новой системе координат уравнение параболы принимает вид

25y2 −

5 (4x1 − 3y1) +

5

(3x1 + 4y1) − 50 = 0, или 25y2 + 100y1+

+50x1 − 50 = 0; 25(y1 + 2)2 = 50(3 − x1); (y1 + 2)2 = 2(3 − x1). Ви-

дим, что параметр p параболы равен единице.

Совершим параллельный перенос осей координат в новое начало

O1 по формулам

Теперь

В системе координат (O1, i1, j1)

парабола имеет уравнение y2 =

= −2x2. Осью симметрии явля- ется прямая y2 = 0, т.е. 3x−

−4y − 10 = 0. Вершина O1 пара- болы находится в точке x2 = 0, y2 = 0, следовательно, её коор- динаты удовлетворяют системе

уравнений

Решая систему, получаем

Рис. 9.7.

18 1

O1,

5 5

- вершину параболы. Теперь можно построить дан-

ную параболу. Для этого в старой системе строим новую систему

координат, а затем строим параболу (рис. 9.7).

Дата добавления: 2015-09-01