Задачи для самостоятельного решения. 9.5.3.Каждое из уравнений

9.5.3. Каждое из уравнений

а) 14x2 + 24xy + 21y2 − 4x + 18y − 139 = 0, б) 11x2 − 20xy − 4y2 − 20x − 8y + 1 = 0,

в) 9x2 + 24xy + 16y2 − 18x + 226y + 229 = 0

приведите к каноническому виду; определите, какие геометрические образы они определяют; укажите координаты центра симметрии и уравнение фокальной оси, если кривая - эллипс или гипербола, и координаты вершины, если кривая парабола; укажите величины по- луосей для эллипса или гиперболы, или величину параметра p для параболы; укажите коорди

96 7. Приложение линейной алгебры

5. Эллиптический параболоид.

При вращении параболы y2 = 2pz плоско- сти Y OZ вокруг оси OZ получим поверх- ность x2 + y2 = 2pz. Поверхность, определяе- мая уравнением

x2 y2

Рис. 7.17.

a2 + b2 = 2pz (p > 0),

называется эллиптическим параболоидом (рис. 7.17). При пересечении эллиптического параболоида плоскостями z = h > 0 получим эллипсы, а плоскостями, параллельными плоскостям XOZ и Y OZ, параболы.

6. Гиперболический параболоид.

Поверхность, определяемая

уравнением

x2 y2

a2 − b2 = 2pz (p > 0),

называется гиперболическим па- раболоидом (рис. 7.18). Его сече- ния
- гиперболы

Рис. 7.18

параболы;

- параболы

7. Конусы второго порядка.

Поверхность, задаваемая уравнением

x2 y2 z2

a2 + b2 − c2 = 0,

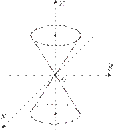называется конусом второго порядка

Это уравнение является однородным второй степени. В сечении плоскостями

z = h получим эллипсы

В сечении плоскостью x = 0 получим две пе

ресекающиеся прямые:

наты новых базисных векторов; в случае параболы запишите уравнение оси симметрии; постройте кривые в старой системе координат.

Ответы: а) эллипс; б) гипербола; в) парабола.

Дата добавления: 2015-09-01