Доходность облигации

Доходность срочной облигации без права досрочного погашения. Оценка стоимости подобной облигации выполняется по формуле (12.3); эта же формула может использоваться для оценки доходности отзывной облигации r. Предполагается, что в этой формуле известны все показатели кроме r напомним, что в левой части (6.3) в этом случае берется текущая рыночная цена актива Р_m:

(6.3)

где CF — сумма регулярно выплачиваемого процентного дохода за базисный период;

n — число базисных периодов до погашения облигации;

М — нарицательная стоимость облигации;

M — нарицательная стоимость облигации;

R_m — рыночная цена облигации на момент ее приобретения.

Доходность срочной облигации с правом досрочного погашения.

Отзывная облигация отличается от безотзывной наличием дополнительных характеристик: 1) выкупной цены P_с которая будет выплачена держателю облигации в случае досрочного ее погашения, 2) срока защиты от досрочного погашения (первые m базисных периодов с момента эмиссии в течение которых отзыв облигации запрещен). Для подобной облигации можно рассчитать доходность на момент ее погашения в срок и на конец m -го базисного периода.

Доходность конвертируемой облигации. Для оценки ожидаемой доходности конвертируемой облигации можно воспользоваться алгоритмами, используемыми в случае с облигациями с правом досрочного погашения, в которых выкупная цена заменена ожидаемой конверсионной стоимостью. Основным моментом анализа в данном случае является установление прогнозной оценки стоимости базисного актива на тот или иной момент времени.

Доходность акции. Доходность акции — это относительный показатель, характеризующий эффективность инвестирования в акцию; обычно рассчитывается в терминах годовой процентной ставки соотнесением годового дохода, приносимого данной акцией, с величиной инвестиции в нее. В общем случае годовой доход состоит из двух компонентов: регулярного дохода, называемого дивидендом, и дохода от капитализации, исчисляемого как разность значений рыночной цены акции на конец и начало года. Соответственно общая доходность акции представляет собой сумму дивидендной доходности и капитализированной доходности.

Теоретически доходность может быть рассчитана на любой момент времени с помощью DCF и представляет собой значение показателя r при условии, что аналитику известны текущая цена акции (левая часть модели) и ожидаемые годовые доходы, т. е. дивиденды (правая часть модели). Поскольку в общем случае дивиденды с течением времени меняются стохастически, модель Уильямса может применяться лишь при условии внесения дополнительных ограничений на их функциональную зависимость и (или) динамику. Наиболее типовые ситуации, допускающие формализованный расчет доходности, таковы: 1) величина дивиденда постоянна (это характерно для привилегированных акций); 2) величина дивиденда меняется с заданным постоянным темпом g.

Доходность акции с постоянным доходом. Возвратный денежный поток представляет собой бессрочный аннуитет, для которого формализованное представление связи внутренней стоимости акции (V_t), выплачиваемых по ней годовых дивидендов (D) и доходности (k) выражается с помощью DCF-модели следующим образом:

(6.4)

Интерпретация этой формулы такова: в условиях равновесного рынка акция с регулярным годовым дивидендом D и годовой доходностью k теоретически должна стоить V_t. Условие равновесности означает, что текущая рыночная цена акции должна соответствовать ее теоретической стоимости, т.е. Р_m=V_t. Отсюда следует, что в условиях равновесного рынка доходность акции может быть исчислена по формуле:

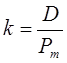(6.5)

где D — ожидаемый дивиденд;

Р_m — рыночная цена на момент оценки.

При принятии решения о целесообразности покупки акции неявно предполагается, что после покупки акции инвестор не предполагает продать ее в ближайшем будущем. Поэтому общая доходность здесь совпадает с текущей дивидендной доходностью. Считается, что такой оценки, в принципе, достаточно для принятия решения; в дальнейшем при необходимости продажи акции могут быть рассчитаны фактические значения других показателей доходности.

Доходность акции с равномерно увеличивающимся доходом. Поскольку одной из особенностей экономики является стремление к росту и, кроме того, в экономике всегда имеют место инфляционные процессы, вполне естественной выглядит предпосылка о том, что одновременно с ростом ресурсного потенциала фирмы должны расти дивиденды, выплачиваемые по ее акциям. Формализации поддается ситуация, когда темп прироста дивиденда постоянен и равен некоторой величине g. В этом случае доходность акции находится путем очевидного преобразования модели Гордона (12.7):

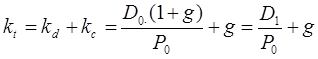(6.6)

где D₀ — последний полученный к моменту оценки дивиденд по акции;

D₁ — ожидаемый дивиденд;

Pо — цена акции на момент оценки;

g — темп прироста дивиденда.

Из формулы (6.6) видно, что ожидаемая капитализированная доходность обыкновенной акции с равномерно возрастающим дивидендом совпадает с темпом прироста дивиденда или с темпом прироста цены акции. Таким образом, показатель g имеет несколько интерпретаций: во-первых, это капитализированная доходность; во-вторых, темп прироста дивиденда; в-третьих, темп прироста цены акции.

Поскольку объективно установить значение g невозможно — его можно задать и искусственно придерживаться в своей дивидендной политике, однако в условиях рынка подобное жесткое ограничение вряд ли реализуемо в течение длительного времени. Кроме того, здесь не учитывается фактор риска, который всегда присущ бизнесу вообще и финансовому рынку в частности: именно этот фактор существенно влияет на ценовую динамику.

Дата добавления: 2015-09-05