Энтропия Шеннона, кол-во информации.

Информацио́нная энтропи́я — мера неопределённости или непредсказуемости информации,

Энтропия — это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

1. мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;
2. в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;
3. должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Поэтому функция энтропии H должна удовлетворять условиям:

1. определена и непрерывна для всех , где 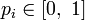для всех и 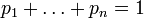. (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)
2. Для целых положительных n, должно выполняться следующее неравенство:

1. Для целых положительных b_i, где , должно выполняться равенство:

Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:

где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии (), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел.

9. Принцип предпочтительности. Ряды предпочтительных чисел.

Принцип предпочтительности – один из основных принципов, используемых в стандартизации. Различают качественный и количественный аспекты применения этого принципа. Качественный аспект состоит в образовании предпочтительных рядов объектов стандартизации.

Уровней предпочтительности может быть как минимум два. В соответствии с уровнями следует выбирать по возможности более предпочтительные объекты. Как правило, наиболее предпочтительный ряд включает наименьшее количество объектов или параметров объектов стандартизации. Следующие, менее предпочтительные ряды отличаются расширенной номенклатурой и могут включать объекты предыдущих рядов. Соблюдение принципа предпочтительности позволяет добиться разумного сокращения применяемой номенклатуры стандартных объектов (элементов). Поскольку в первую очередь выбирают из наиболее предпочтительного ряда (1) и переходят к менее предпочтительным (2, 3 и др.) только если поставленная задача не имеет удовлетворительного решения на более высоком уровне, то при наличии необходимого разнообразия стандартных объектов (элементов) существенно сокращается число наиболее часто используемых решений. Стандартом установлены пять рядов R, называемых иногда рядами Ренара, которые построены на основе геометрической прогрессии со знаменателем в виде корня определенной степени из десяти (табл. 1). Ряды R5…R40 называются основными, ряд R80 – дополнительным. Наиболее предпочтительным является ряд R5, за ним следует ряд R10, и т.д. Дополнительный ряд R80 можно применять только в технически и экономически обоснованных случаях.

Структура знаменателей рядов предпочтительных чисел

Ряд	Знаменатель
R5	5 __ √10 ≈ 1,5949 (приблизительно 1,6)
R10	10 __ √10 ≈ 1,2589 (приблизительно 1,25)
R20	20__ √10 ≈ 1,1220 (приблизительно 1,12)
R40	40__ √10 ≈ 1,0593 (приблизительно 1,06)
R80	80 __ √10 ≈ 1,0292 (приблизительно 1,03)

Дата добавления: 2015-09-05