Представление чисел с плавающей запятой

Представление чисел с плавающей запятой основывается на изображении чисел в полулогарифмической форме с использованием пары значений (± р, ± М), что соответствует записи чисел в нормальной форме в виде A = d^±p· (±М), где d - основание системы счисления; р - целое число, называемое порядком числа А; М - мантисса числа А (обычно |М|<1).

Фактически положение запятой в мантиссе М определяется величиной порядка р. С изменением р в большую или меньшую сторону запятая соответственно перемещается влево или вправо, т. е. «плавает» в изображении числа.

Пример 7.1. Представить в форме с плавающей запятой числа 158₁₀ и 101101₂.

Решение:

1. 158₁₀ = 10³ · 0,158 = 10⁴ · 0,0158 = 10⁵ · 0,00158;

2. 101101₂ = .

Числа, удовлетворяющие условию 1/d≤М<1, называют нормализованными.

Как показано на рисунке 3.2, в разрядной сетке ЭВМ фиксируются знак числа, знак порядка, порядок числа и числовое выражение мантиссы.

В памяти ЭВМ числа хранятся нормализованными. Нормализованное представление чисел позволяет сохранять в разрядной сетке большое количество значащих цифр, что повышает точность вычислений.

					m	m+1	m+2		m+n+1
a0	β 0	β2	β3	…	βm	a1	a2	…	an
Знак числа	Знак порядка

Рисунок 7.2 – Разрядная сетка ЭВМ для представления чисел с плавающей запятой

Обычно в ЭВМ нормализация осуществляется автоматически как при вводе чисел, так и в процессе вычислений (после выполнения очередной операции). При этом мантисса может сдвигаться влево на необходимое число разрядов (увеличиваться); при этом производится соответствующее уменьшение порядка, т.е. выполняется «нормализация влево».

При выполнении операций над числами с плавающей запятой возможно переполнение разрядной сетки, так же как и с числами с фиксированной запятой. В таком случае появляется единица слева от запятой. Такого рода переполнение исключается сдвигом мантиссы вправо на один разряд и увеличением порядка на единицу, т. е. производится «нормализация вправо».

От количества разрядов, отводимых для хранения порядка, зависит диапазон записываемых чисел, а от количества разрядов, отводимых для мантиссы,- точность записи числа. Если под цифровые разряды мантиссы отведено n, а порядка - т разрядов, то максимальное и минимальное по абсолютной величине нормализованные двоичные числа соответственно равны:

,

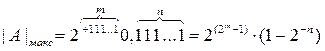Диапазон чисел с плавающей запятой определяется неравенством:

При достаточно больших n (обычно n³30) – 1-2ⁿ » 1 и неравенство принимает вид:

Из этого неравенства видно, что диапазон чисел зависит в основном от порядка р. Если число превышает верхний предел неравенства, то происходит переполнение разрядной сетки и ЭВМ автоматически останавливается. Если число выйдет за нижний предел неравенства, то оно будет соответствовать машинному нулю.

Дата добавления: 2015-08-27