Представление чисел с фиксированной точкой

Число с фиксированной точкой - естественная форма представления числа, когда положение точки в разрядной сетке ЭВМ строго фиксируется (размер разрядной сетки соответствует длине машинного слова). Обычно она фиксируется перед старшим или после младшего разрядов. Если точка фиксируется перед старшим разрядом, то числа в ЭВМ представляются как правильные дроби; если после младшего - как целые числа.

Схематично разрядная сетка ЭВМ для представления чисел с фиксированной запятой представлена на рисунке 3.1.

Знак	2^-1	2^-2	2^-3	2^-4		2^-^(n-3)	2^-^(n-2)	2^-^(n-1)	2^-^n
a0	a1	a2	a3	a4	…	an-3	an-2	an-1	an
						n-3	n-2	n-1	n
				а)

Знак	2^n-1	2^n-^2	2^n-^3	2^n-4		2^3	2^2	2^1	2^0
a0	a1	a2	a3	a4	…	an-3	an-2	an-1	an
						n-3	n-2	n-1	n
				б)

Рисунок 7. 1 – Разрядная сетка ЭВМ для представления чисел с фиксированной точкой: а) перед старшим разрядом; б) после младшего разряда

В разрядной сетке ЭВМ для представления чисел с фиксированной точкой разряды нумеруются слева направо, начиная с нулевого, который называется знаковым разрядом. В этом разряде 0 соответствует плюсу, а 1 - минусу. На рисунке 3.1 указан вес каждого разряда.

Максимальное абсолютное значение (т.е без учета знака) дробного числа (рисунок а)) очевидно будет равно:

|Х|_макс = 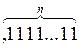= 1-2^-n

где n - количество разрядов числа.

Минимальное, отличное от нуля машинное число будет равно:

|Х|_мин = 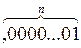= 2^-n.

Диапазон чисел всех возможных величин в данном случае определяется неравенством:

2^-n≤|Х|≤(1-2^-n).

Анализируя это неравенство, можно отметить следующее:

1. Диапазон представления чисел в машинах с фиксированной запятой сравнительно невелик.

2. Число, абсолютное значение которого меньше минимального машинного слова (2^-n), будет записано в ЭВМ в виде нуля. Такое число называется машинным нулем, так как на самом деле оно не равно нулю, но для его изображения недостаточно разрядов в машинном слове.

3. Число, полученное в результате вычислений по абсолютному значению, не должно превышать максимального машинного числа (1-2^-n). Если число выходит за верхний предел (1-2^-n), то целая часть его не может быть расположена в машинном слове и поэтому теряется, что приводит к искажению результата. В этом случае говорят, что произошло переполнение разрядной сетки.

4. Относительная погрешность вычислений δ тем больше, чем меньше по абсолютной величине числа, участвующие в вычислениях, так как δ = Δ/ А · 100, где Δ - абсолютная погрешность; А - двоичное число. Если в ЭВМ имеется n разрядов числа, то абсолютная погрешность определяется точностью ее последнего знака, т. е. в данном случае А = 2^-n.

Например, при n = 4 для числа A = 0,1111 относительная погрешность составит

δ _мин = [2^-4 / (15/16)] · 100% = 6,7%,

а для числа А=0,0001

δ _макс = [2^-4 / (1/16)] ·100% = 100%.

Если запятая фиксирована после младшего разряда (рисунок б)), разрядная сетка позволяет представлять отрицательные и положительные двоичные числа, модуль которых 1 ≤ |Х| ≤ (2ⁿ-1), где n - количество числовых разрядов в разрядной сетке ЭВМ. Все числа, модуль которых меньше 1 или больше (2ⁿ-1), не могут быть представлены в этой разрядной сетке.

Среди команд ЭВМ есть такие, когда операция с фиксированной запятой производится не только над числами, но и над адресами. В этом случае операнд интерпретируется как двоичное число без знака. Диапазон представления чисел без знака в два раза больше, чем со знаком в разрядной сетке ЭВМ.

Дата добавления: 2015-08-27