Общие сведения о системах счисления

АРИФМЕТИЧЕСКИЕ ОСНОВЫ ВТ (К.А. Нешумова ЭВМ и системы, 1989)

Общие сведения о системах счисления

Система счисления - совокупность приемов и правил для изображения чисел с помощью символов (цифр), имеющих определенные количественные значения. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные. В ЭВМ применяются позиционные системы счисления. Непозиционные системы счисления в ВТ не используются из-за своей громоздкости и сложности правил образования.

Непозиционной системой счисления называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ею позиции (места) в изображении числа, а определяется лишь самим символом (цифрой). Так, например, в римской системе счисления число XXX содержит во всех разрядах один и тот же символ X, который означает 10 единиц независимо от его позиции в изображении числа.

Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от ее позиции (места) в числе. Примером может служить обычная десятичная система счисления. Например, число 373, представленное в десятичной системе счисления, имеет в младшем и самом старшем разрядах цифру 3. Цифра 3 в старшем разряде имеет вес в 100 раз больше, чем в младшем разряде.

Количество знаков или символов, используемых для изображения числа в данной позиционной системе счисления, называется основанием системы счисления d. Цифры принимают значения от 0 до d -1.Для десятичной системы счисления d = 10 и цифры принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

В общем случае в позиционной системе счисления с основанием d любое число X, может быть представлено в виде полинома от основания d:

(1.1)

где в качестве коэффициента a _i могут стоять любые из d цифр.

Принято представлять числа в виде последовательности соответствующих (1.1) цифр:

(1.2)

Позиции цифр, отсчитываемые от запятой, называются разрядами.

Примеры записи чисел в виде полинома:

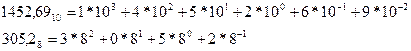
Использование в ЭВМ позиционных систем счисления позволяет значительно упростить изображение чисел и операции с ними.

Дата добавления: 2015-08-27