
Читайте также:
|
Резисторы соединены последовательно, если по ним течет один и тот же ток. Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме их сопротивлений:
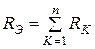 . .
| (1.1) |
Резисторы соединены параллельно, если они подключены к одной и той же паре узлов. Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных резисторов, определяется из выражения:

| (1.2) |
В частном случае параллельного соединения двух резисторов эквивалентное сопротивление находится по формуле:
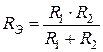 . .
| (1.3) |
Если параллельно соединены n одинаковых резисторов, то их эквивалентное сопротивление в n раз меньше одного из них:
 .
.
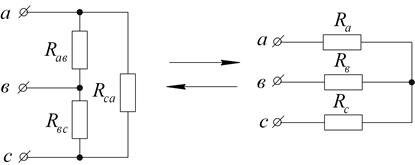
Преобразование треугольника резисторов в эквивалентную звезду и наоборот проводится по следующей схеме и формулам:
  
| (1.4) |
 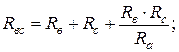 
| (1.5) |
ПРИМЕР 1.1.1
Дано:  Ом;
Ом;  Ом;
Ом; 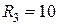 Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 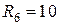 Ом;
Ом; 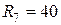 Ом;
Ом;  Ом.
Ом.
Определить:  .
.

Решение: Заменим треугольники авс и dfg эквивалентными звездами.

 Ом;
Ом;  Ом;
Ом;
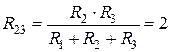 Ом;
Ом;  Ом;
Ом;
 Ом;
Ом; 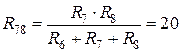 Ом.
Ом.

Резисторы R 13, R 4, R 67 и R 23, R 5, R 68 соединены последовательно, поэтому  Ом;
Ом;  Ом.
Ом.
Резисторы R 9 и R 10 параллельны, следовательно,  Ом.
Ом.
Входное сопротивление цепи  Ом.
Ом.
ПРИМЕР 1.1.2
Дано:  Ом.
Ом.
Определить:  .
.

Решение: Если в ветви, соединяющей два узла, сопротивление отсутствует, то потенциалы этих узлов одинаковы  , при
, при  ,
,  .
.
Такие узлы целесообразно обозначать одинаковыми буквами или цифрами и схему перечертить так, чтобы каждый узел на ней изображался только один раз.
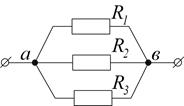
Решение: Узлы 1 и 3 соединены проводом, сопротивление которого равно нулю. Потенциалы этих узлов одинаковы, поэтому обозначим их буквой а. Аналогично, узлы 2 и 4 обозначим буквой в. Перечертим схему.
Резисторы R 1, R 2, R 3 параллельны, их эквивалентное сопротивление 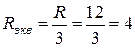 Ом.
Ом.
ЗАДАЧИ
1.1.1. Дано:  .
.

Определить:  .
.
1.1.2. Дано: 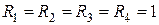 Ом,
Ом,  Ом.
Ом.
Определить:  .
.

1.1.3. Дано:  Ом,
Ом,
 Ом
Ом
. 
Определить:  .
.
1.1.4. Дано: 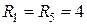 Ом,
Ом,  Ом,
Ом,  Ом.
Ом.

Определить:  .
.
1.1.5. Дано: 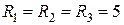 Ом.
Ом.

Определить:  .
.
1.1.6. Дано: 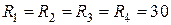 Ом.
Ом.

Определить:  .
.
1.1.7. Дано:  Ом
Ом
. 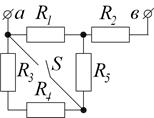
Определить сопротивление R ав при разомкнутом и замкнутом ключе S.
1.1.8. Дано: 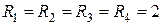 Ом,
Ом, 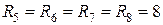 Ом.
Ом. 
Определить:  .
.
1.1.9. Дано: 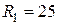 Ом;
Ом;  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом.
Ом. 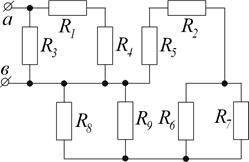
Определить:  .
.
1.1.10. Дано: 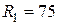 Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.

Определить:  .
.
1.1.11. Дано:  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.

Определить:  .
.
1.1.12. Дано:  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.

Определить:  .
.
1.1.13. Дано: 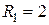 Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 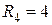 Ом;
Ом;  Ом;
Ом;  Ом.
Ом. 
Определить:  .
.
1.1.14. Дано: 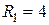 Ом;
Ом;  Ом;
Ом;  Ом.
Ом.

Определить:  .
.
1.1.15. Дано:  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.
Определить:  .
.
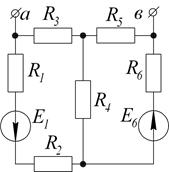
1.1.16. Дано:  Ом;
Ом;  Ом.
Ом.

Определить сопротивление нагрузки источника.
Дата добавления: 2015-08-27; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Методические указания к компьютерному моделированию задания Модуля 1 | | | Метод преобразования (свертывания) цепей |