Задание 5. Решить операционным методом систему уравнений и проверить решение:

Решить операционным методом систему уравнений и проверить решение:

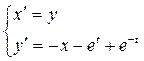
Решение:

Переходим от оригиналов к изображениям с помощью теоремы о дифференцировании оригинала:

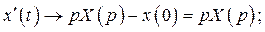
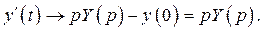
Учитывая, что , получим операторную систему:

Разложим правильную дробь на простейшие дроби:

Приравняем коэффициенты при одинаковых степенях в правой и левой части равенства и получим систему для нахождения коэффициентов :

Аналогично разложим правильную дробь 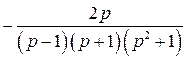на простейшие дроби:

Приравняем коэффициенты при одинаковых степенях в правой и левой части равенства и получим систему для нахождения коэффициентов :

Следовательно,

Пользуясь таблицей изображений, находим решение системы:

Выполним проверку решения, для чего вычислим и :

Подставим выражения 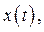и в исходную систему:

В результате проверки получены тождественные равенства в обоих уравнениях системы, следовательно, решение найдено верно.

Ответ:

Дата добавления: 2015-08-27