Задание 3. Найти изображение дифференциального выражения и функции:

Найти изображение дифференциального выражения и функции:

если

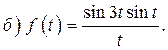
Решение:

а) Пользуясь теоремой о дифференцировании функции-оригинала , находим

Тогда, используя свойство линейности, получим искомое изображение дифференциального выражения:

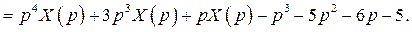
Ответ: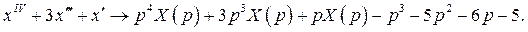

б) Выполним следующее преобразование:

Используя табличные соответствия оригиналов изображениям, находим:

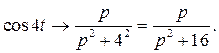
Тогда, используя свойство линейности, получим

Применяя теорему интегрирования изображения, находим:

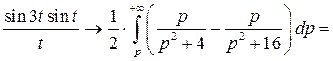
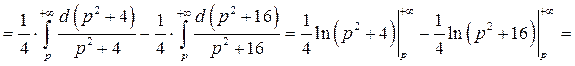
Таким образом, искомое изображение функции 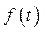имеет вид:

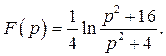
Ответ: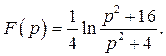

Дата добавления: 2015-08-27