Задание 4. Решить операционным методом уравнения и проверить решения:

Решить операционным методом уравнения и проверить решения:

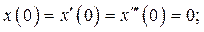
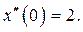
Решение:

а) Переходим от оригиналов к изображениям с помощью теоремы о дифференцировании оригинала:

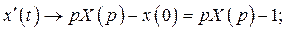
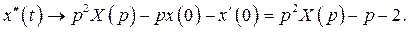
Операторное уравнение имеет вид:

Решаем операторное уравнение относительно :

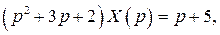
откуда находим

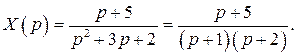
Разложим правильную дробь 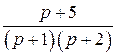на сумму простейших дробей методом неопределённых коэффициентов:

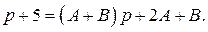
Приравняем коэффициенты при одинаковых степенях в правой и левой части равенства и получим систему для нахождения коэффициентов А и В:

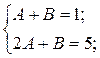
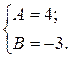
Следовательно,

Возвращаемся к оригиналам, получим частное решение исходного дифференциального уравнения:

Выполним проверку решения, для чего определим и :

Подставим выражения и в исходное дифференциальное уравнение:

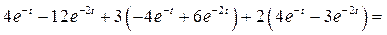
В результате проверки получено тождественное равенство, следовательно, уравнение решено верно.

Ответ:

б) Переходим от оригиналов к изображениям с помощью теоремы о дифференцировании оригинала:

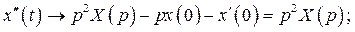
Находим изображение правой части уравнения:

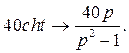
Операторное уравнение имеет вид:

Решаем операторное уравнение относительно :

откуда находим

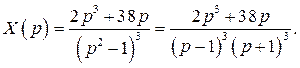
Разложим правильную дробь на сумму простейших дробей методом неопределённых коэффициентов:

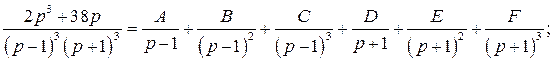
Приравняем коэффициенты при одинаковых степенях в правой и левой части равенства и получим систему для нахождения коэффициентов :

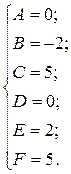
Следовательно,

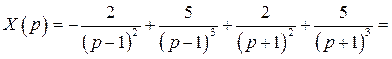
Возвращаемся к оригиналам, получим частное решение исходного дифференциального уравнения:

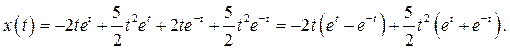
Выполним проверку решения, для чего вычислим:

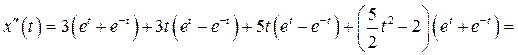
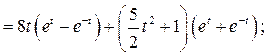
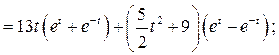
Подставим выражения и в исходное дифференциальное уравнение:

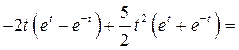
В результате проверки получено тождественное равенство, следовательно, уравнение решено верно.

Ответ:

Дата добавления: 2015-08-27