|
Читайте также: |
Будет ли функция оригиналом в преобразовании Лапласа? Ответ пояснить.
Решение:
Проверим выполнение следующих условий:
1. Заданная функция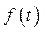 
локально интегрируема, т.е. интеграл 
существует для любых конечных 
и 
.
2. Условие того, что для всех отрицательных 
значение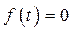 
, выполнено в силу задания функции.
3. 
возрастает при 
не быстрее показательной функции, т.е. существуют такие постоянные 
и 
, что для любых вещественных справедливо неравенство 
. В данном случае можно взять любые 
и 
.
Поскольку заданная функция 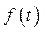удовлетворяет всем трём условиям, то она является функцией-оригиналом по определению.
Ответ: да.
Дата добавления: 2015-08-27; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Publishers Weekly | | | Задание 2 |