Теорема 3.1

Элементарные преобразования не изменяют ранга матрицы.

Теорема 3.2 (О ступенчатой матрице):

1). Каждая матрица элементарными преобразованиями строк приводится к ступенчатой матрице.

2). Ранг ступенчатой матрицы равен числу ненулевых строк.

Доказательство

1) Возьмем первый слева столбец, содержащий ненулевые элементы.Переставим строки матрицы так, чтобы один из ненулевых элементов этого столбца оказался в первой строке (если первый элемент взятого столбца был равен нулю).

С помощью преобразований строк можно получить новую матрицу, в которой все элементы под 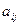окажутся равными нулю. Чтобы получить нуль на месте элемента 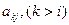, достаточно умножить 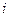-ю строку матрицы (где стоит 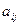) на число и прибавить к -ой строке (где стоит ). Действительно, на месте элемента получим

Обратим указанным способом в нуль все элементы под этим ненулевым элементом. Первая строка ступенчатой матрицы готова: все ненулевые элементы второй и нижних строк теперь стоят правее первого ненулевого элемента первой строки. Применим ту же операцию к матрице, начинающейся со второй строки и так далее. Так как строк – конечное число, то в результате получим ступенчатую матрицу.

2). Пусть в ступенчатой матрице имеется ненулевых строк. Тогда каждый минор -го и высшего порядка содержит нулевые строки (хотя бы одну) и потому равен нулю. Но имеется хотя бы один минор -го порядка отличный от нуля: наверняка треугольный минор не равен нулю, главную диагональ которого образуют первые ненулевые элементы всех ненулевых строк. Действительно, такой минор равен произведению элементов главной диагонали и поэтому не равен нулю. Значит .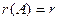

Пример 3.3. Придумать ступенчатую матрицу шестого порядка, чтобы .

.

Пример 3.4. Определить ранг матрицы:

1) методом «окаймляющих миноров»:

2) приведением матрицы к ступенчатому виду.

2)

Дата добавления: 2015-08-27