
Читайте также:
|
Каждый отличный от нуля минор, порядок которого совпадает с рангом матрицы, называется базисным минором.
Сколько может быть базисных миноров у матрицы? (несколько)
В матрице из примера 3.1 все миноры 3-го порядка равны ___ нулю ______,
(Проверить.)
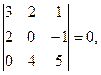



но имеются отличные от нуля миноры 2-го порядка, значит, 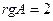 .
.
Правило вычисления ранга матрицы (метод «окаймляющих миноров»).
При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор k-го порядка D, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D: если все они равны нулю, то ранг матрицы равен k.
. 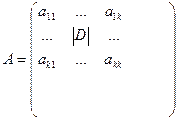 .
.
Матрица большого размера имеет много миноров различных порядков и нахождение ранга только на основании определения 3.2 (перебором всех возможных миноров) или даже методом «окаймляющих миноров» требует много времени. Эта задача существенно упрощается с помощью перехода от данной матрицы так называемыми элементарными преобразованиями к ступенчатой матрице:
Дата добавления: 2015-08-27; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение 3.2 | | | Теорема 3.1 |