Частотные передаточные функции и частотные характеристики

Если на вход линейного звена (рис. 1.3, а) подать синусоидальный сигнал x = A₁sinωt с круговой частотой ω и амплитудой А₁, то на выходе звена появятся установившиеся колебания y = A₂( ω )sin [(ω) t+ φ(ω)] той же частоты, но другой амплитуды Α₂ и сдвинутые по фазе на угол φ(ω₁) (см. рис. 1.3, а).

Сдвиг фазы выходного сигнала φ(ω) = - (2πΔ t/T), φ (ω)—называется фазово-частотной характеристикой (ФЧХ), а выраже-

ние A (ω) =A₂(ω)/A₁(ω) – называется амплитудно-частотной ха-

рактеристикой (АЧХ).

Значения частотных характеристик определяются по передаточным функциям с переходом от преобразования Лапласа

к преобразованию Фурье, заменой Ρ = j ω, j = √-1, ω =2π/ T –

частота. Из рис. 1.3, a передаточная функция звена К(Р) = =Y(P)/X(P). Заменим Ρ = j ω, получим выражение частотной передаточной функции звена

(1.19)

где U(ω) —вещественная и jV (ω)—мнимая часть частотной передаточной функции W(j ω).

Графическая интерпретация частотной передаточной функции на комплексной плоскости в координатах U (ω) и jV (ω) представляет собой амплитудно-фазовую частотную характеристику (АФЧХ), которая показана на рис. 1.3,б. Для построения АФЧХ необходимо вычислить U (ω) и jV (ω) при ω = 0; 0,01; 0,1; 1; 10; 100;...; ∞. АФХЧ показывает, что с увеличением частоты входного сигнала линейных звеньев уменьшается амплитуда и возрастает сдвиг фазы выходного сигнала. АФЧХ дает

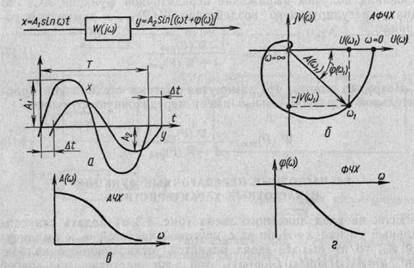
Рис. 1.3. Частотные характеристики звеньев и систем автоматики

исчерпывающие характеристики фильтрующих и фазовых свойств того или иного элемента или системы автоматики. Из рис. 1.3,б нетрудно получить формулы отдельного вычисления АЧХ и ФЧХ·

(1.20) (1.21)

Для элементов автоматики с линейной статической характеристикой амплитудно-частотные и фазово-частотные характеристики представлены на рис. 1.3, в, г. Рис. 1.3 и формулы (1.20) и (1.21) характеризуют связь частотной передаточной функции W(j ω ) с амплитудной и фазовой частотной характеристикой

(1.22)

Определим частотные характеристики разомкнутой системы из цепи последовательно соединенных звеньев автоматики.

В формуле (1.14) заменим Ρ = j ω, получим W(j ω)_раз = = W₁ (jω)... W_n(j ω ), заменим W(j ω)_раз выражением (1.22), находим

(1.23)

В разомкнутой системе из последовательно соединенных звеньев амплитуда (модуль) АФЧХ равна произведению модулей звеньев, а сдвиг фазы — сумме сдвигов фаз отдельных звеньев.

Частотные характеристики звеньев, систем дают возможность определить запасы устойчивости АСР по фазе и амплитуде, вычислить оптимальные настройки регуляторов и параметры корректирующих устройств АСР, а также решать другие задачи анализа и синтеза систем автоматики.

Дата добавления: 2015-08-27