Классификация элементов автоматики

Все многообразие автоматических, автоматизированных систем строится на использовании определенных элементов, устройств автоматики, которые реализуют заданные им функции. Подбор элементов автоматики при соответствующей их компоновке образует систему того или иного назначения. Интенсивное развитие элементной базы различной физической природы дало возможность промышленности освоить массовый выпуск элементов, устройств автоматизации, которые можно разделить на аналоговые и цифровые.

Аналоговые элементы — это элементы, создающие разнообразные аналоговые системы автоматики. В них входная информация преобразуется в выходную информацию в виде аналоговых сигналов — электрического напряжения, тока, емкости, индуктивности, давления сжатого воздуха, жидкости, углов поворота, линейных перемещений и т. д., т. е. в элементе автоматики изменению входной величины соответствует изменение его физического аналога выходной величины. Закон изменения выходной величины зависит от назначения элемента автоматики. Простейшие устройства аналоговой автоматики известны более 2000 лет тому назад.

Цифровые элементы автоматики появились сравнительно недавно. Одним из первых распространенных цифровых устройств автоматики стал телеграфный аппарат, в котором входная буквенно-числовая информация преобразуется в цифровой код чередования электрических импульсов, который передается по проводным линиям к приемнику дешифратора кода.

В цифровых элементах автоматики происходит изменение не аналоговых сигналов, а изменение структур, последовательностей электрических импульсов («1» и «0») цифровых двоичных, восьмеричных, двоично-десятичных и других кодов. Цифровые системы автоматики способны решать очень сложные задачи автоматизации, недоступные возможностям аналоговых систем.

Массовое производство цифровых интегральных микросхем разной степени интеграции обеспечивает широкие перспективы развития средств и систем цифровой автоматики.

По своему назначению все аналоговые, а также многие цифровые элементы автоматики можно разделить на ряд групп:

воспринимающие элементы (датчики)—это преобразователи контролируемых или регулируемых величин в выходные сигналы, удобные для дистанционной передачи и дальнейшей обработки; датчики служат прежде всего для контроля за изменением технологических параметров: размеров лесоматериалов, влажности древесины, температуры и давления среды, расхода энергии, сырья и т. д.;

усилительные элементы представлены в виде устройства, в которых осуществляется увеличение мощности управляющего (входного) сигнала за счет энергии вспомогательного (управляемого) источника питания, причем связь между выходным и входным сигналами непрерывная и однозначная; усилители бывают разных физических принципов;

исполнительные элементы — это устройства, которые по командному сигналу воздействуют на объект управления, изменяя величину потока энергии или материала посредством перемещения регулирующего органа;

релейные элементы представляют собой устройства, в которых непрерывное изменение входной величины вызывает скочкообразное изменение выходной величины; релейные элементы дают возможность при помощи малых мощностей управлять распространением больших мощностей;

логические элементы осуществляют определенные логические зависимости между входными и выходными сигналами; используются для построения дискретных систем автоматического контроля, управления, а также для создания различных устройств, блоков цифровой автоматики;

регулирующие и управляющие элементы (устройства) служат для стабилизации или изменения по соответствующему алгоритму, программе параметров процессов; они включают в себя устройства широкого диапазона, от простейших кнопок управления, простых регуляторов прямого действия до управляющих цифровых вычислительных машин.

1.3. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ

В элементах автоматики статические характеристики выражают связь между выходной у и входной величиной χ в установившихся, статических режимах (рис. 1.1).

На рис. 1.1,а представлена прямолинейная статическая характеристика вида y = kx, k = tgα, которую имеют различные датчики, многие усилители, механические передачи. На рис. 1.1,б показана непрямолинейная характеристика. Сюда относятся термопары, клапана. Зависимость между напряжением на якоре и током возбуждения электрической машины при постоянной скорости вращения представлена на рис. 1.1,в и выражается зависимостью:

у = 0 при | x | < 0

k = tgα y = k(x—a) при x > + а (1.1)

y = k{x + a) при x < - а.

Примером служат механические передачи с зазором 2а, некоторые золотниковые гидрораспределители.

На рис. 1,1,г приведена релейная характеристика, отвечающая следующей зависимости

у = 0 при | x | <а, | у | = В при | x | >а (1.2)

Эта характеристика относится к электронным, электриче-

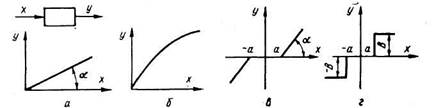
Рис. 1.1. Статические характеристики элементов автоматики

ским релейным устройствам. Существует реле, у которых зона нечувствительности 2а = 0.

Статические характеристики цифровых элементов автоматики описываются соответствующими формулами алгебры логики.

1.4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА

При анализе, синтезе элементов и систем автоматики приходится оперировать со сложными дифференциальными уравнениями. В связи с этим для упрощения расчетов целесообразно вспомнить и применить аппарат операционного исчисления, в основе которого лежит преобразование Лапласа. Это преобразование дает возможность заменить операции дифференцирования и интегрирования операциями умножения и деления, а также достаточно просто решать задачи анализа и синтеза систем автоматики.

Пусть y(t) —функция независимой вещественной переменной. Изображением по Лапласу Y(P) оригинала y(t) называется интеграл

(1.3)

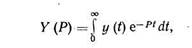
(1.3)

где Ρ = α + j β — комплексная величина.

Интеграл (1.3) является функцией комплексного аргумента. Функциональное преобразование вида (1.3) имеет сокращенное обозначение Y(P)÷→y(t) или y(t)←÷Y(P). При нулевых начальных условиях комплексная переменная Ρ может быть отождествлена с операцией дифференцирования, т. е. Р = = d/dt.

Без доказательства рассмотрим основные свойства преобразования Лапласа.

1. При преобразовании Лапласа значения функции y(t) рассматриваются только при t >0, т. е. после приложения к элементу системы внешних воздействий, например управляющего воздействия g(t) на автоматическую систему регулирования (АСР). А это и представляет интерес для анализа и синтеза АСР. Поэтому у (t) = 0 при t <0.

Уместно отметить, что при t = 0, Р = ∞ и при t = ∞, Р = 0.

2. При умножении оригинала на постоянную величину а изображение умножается на ту же постоянную и наоборот, т. е.

ay (t) ←÷ aΥ (Ρ). (1.4)

3. Изображение алгебраической суммы конечного числа оригиналов равно сумме их изображений, т. е., если

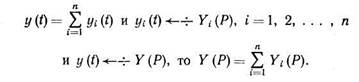
(1.5)

Это свойство позволяет находить изображение (или оригинал) любой линейной комбинации соответствующих функций.

4. Операция дифференцирования оригинала при нулевых начальных условиях соответствует умножению изображения на величину Р, y'(t)<^-±- PY(P), для производных /г-го порядка

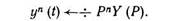
(1.6)

5. Интегрирование оригинала функции в пределах от 0 до t будет соответствовать делению изображения на величину Р:

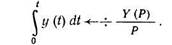
(1.7) 6. Теорема о начальном значении оригинала функции y(t)

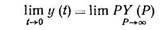
(1.8)

позволяет определить состояние элементов и систем автоматики до приложения внешнего воздействия.

7. Теорема о конечном значении оригинала y{t)

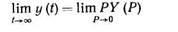
(1.9)

определяет состояние элементов и систем автоматики после затухания переходных процессов, вызванных внешним воздействием.

---

Дата добавления: 2015-08-27