Передаточные функции элементов и систем автоматики

Будем полагать, что движение элементов, систем автоматики описывается линейным дифференциальным уравнением с постоянными коэффициентами (а₀, а₁..., а_n; b₀, b₁,..., b_m) пo входному (управляющему) воздействию g(t)

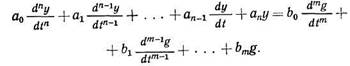
(1.10)

Запишем это уравнение в операторной форме при нулевых начальных условиях

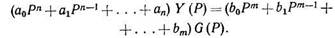
(1.11)

Выполним преобразование уравнения (1.11):

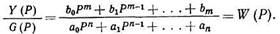
(1.12)

Отношение изображения по Лапласу выходной величины к изображению входной величины и называется передаточной функцией системы (или элемента).

Знаменатель передаточной функции W(P), приравненный нулю, называется характеристическим уравнением системы или элемента автоматики D(P).

D(Ρ) = а₀Р^п + а₁Р^п-1 +... + а_п-1Р + а_п = 0. (1.13)

Рассмотрим передаточную функцию системы из n последовательно соединенных звеньев (рис. 1.2, а). Определим передаточные функции отдельных звеньев (элементов):

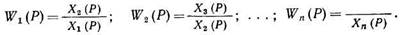
Перемножим передаточные функции звеньев

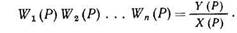
После сокращения получим выражение передаточной функции разомкнутой системы последовательно соединенных звеньев W(P)_раз.

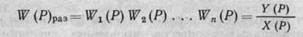
(1.14)

как отношение изображения выходного сигнала Y(P) к изображению входного сигнала Х(Р) системы.

Пусть система состоит из n параллельно соединенных звеньев (рис. 1.2,б). Очевидно, что входной сигнал x(t) и его

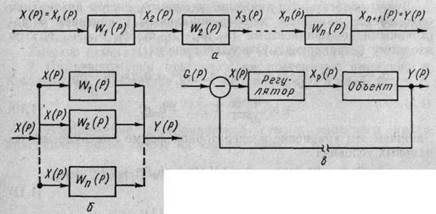
Рис. 1.2. Структурные схемы автоматических систем

изображение X(Р) будет одинаковым для всех n -параллельно включенных звеньев. Выходные сигналы y₁(t); y₂(t);...; y_n(t), а следовательно и их изображения будут различными, так как передаточные функции W₁(P); W₂(P);...; W_n(P) зависят от параметров характеристик звеньев. По правилу сложения запишем y(t)—y₁(t)+y₂(t)+... + y_n(t), с учетом линейности изображений (1.5) справедливо также Y(P) = Y₁(Ρ) +... + Υ_n(Ρ) или Y(P) = W_l(P)X(P) + W₂(P)X(P)+... + W_n(P)X(P). Разделим это выражение на Х(Р), получим

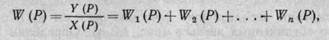
(1.15)

т. е. передаточная функция системы параллельно соединенных звеньев представляет собой сумму передаточных функций отдельных звеньев.

Определим передаточные функции автоматической системы регулирования (АСР) в разомкнутом и замкнутом состоянии. На рис. 1.2, в показана АСР с разомкнутой отрицательной обратной связью. Передаточные функции: регулятора W (Р)_рег =

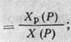
объекта

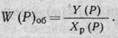
АСР в разомкнутом

состоянии

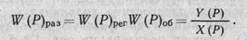
(1.16)

Замкнем регулятор и объект единичной отрицательной обратной связью, т. е. X(P) = G(P)-Υ(Ρ). Подставим это выражение в формулу (1.16)

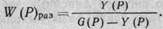
После преобразования получим выражение передаточной функции АСР по каналу регулирующего воздействия W (Ρ) _зам в замкнутом состоянии

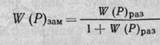
(1.17)

Нетрудно понять, что замкнутая система с единичной положительной обратной связью имеет передаточную функцию

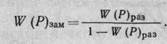
(1.18)

Дата добавления: 2015-08-27