Способы компенсации и учета погрешности

Во всех случаях погрешность датчика стремятся уменьшить. Иногда ее удается полностью или частично скомпенсировать, если же компенсация невозможна, погрешность учитывают и вводят в паспорт датчика.

Источники систематической погрешности могут быть очевидными, не­посредственно вызываемыми условиями работы (например, вибрациями), а могут быть «скрытыми» от прямой регистрации. В последнем случае необ­ходимо, чтобы влияющая функция изменялась во времени, так как тогда систематическую погрешность можно найти и компенсировать. Иначе ее очень сложно обнаружить, единственным способом является периодическая поверка нуля и чувствительности по образцовым мерам.

Для компенсации систематической погрешности на практике используют три основных способа: аналитический, методический и схемотехнический.

Аналитический способ основан на введении в исходную формулу из­вестных аналитических выражений. Например, для датчиков на основе ме­таллических ЧЭ, функция преобразования зависит от температуры:

В общем случае у = Sx или для производных

При х≠ 𝑓(T) имеем

Пусть известна температурная чувствительность первичного преобразо­вателя S_T = ∂S /∂Т. Тогда

Зная реальную температуру датчика, можно определить ΔТ = Т - T_ном и, заменив dT на ΔТ получить окончательно

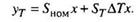
Второе слагаемое в правой части этого выражения представляет собой по­правку к результату измерения.

Характерным примером методического способа является компенсация погрешности, вызванной магнитным полем Земли. Измерения проводят дважды: при любом положении датчика и при изменении его ориентации на 180° относительно предыдущего положения.

Схемотехнический способ предполагает такое построение датчика, при котором отдельные составляющие полной погрешности взаимно компенсируются. Для этого можно использовать, например, симметричные мостовые схемы, частично компенсирующие температурную погрешность.

Рассмотрим этот способ подробнее. Функция преобразования симметричного тензорезистивного моста Уитстона (рис. 1.7) определяется выражением.

где ε — ЭДС источника питания; S_R — чувствительность плеча моста; R₁,R₄ и R₂,R₃

— противолежащие плечи моста.

Стрелками показаны условные направления деформаций под действием влияющих факторов.

Изменение температуры вызывает отклонение сопротивлений плеч моста от их номинальных значений. Тогда получаем

Если ΔR₁= ΔR₂= ΔR₃= ΔR₄, то U_вых1 =U_вых.

Случайная погрешность приводит к разбросу результатов при повторных измерениях. Часто ее компенсация представляет собой сложную задачу, однако иногда разброс можно устранить защитой измерительного канала. С этой целью используют температурную и вибрационную изоляции, электромагнитное экранирование и пр. Существует ряд схемотехнических решений — симметричные дифференциальные схемы, корреляционные методы обработки результатов и т. д. Примером дифференциальной схемы является измерительный мост, позволяющий компенсировать синфазную случайную погрешность (если ее источник действует одновременно на все четыре плеча моста). Если же случайную погрешность устранить не удается, используют статистическую обработку результатов измерений в целях определения наиболее вероятного значения измеренной величины и погрешности датчика. Результаты измерений и их расхождение характеризуют следующие показатели:

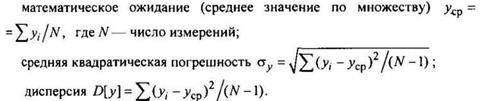
Если погрешности различных измерений независимы между собой, то вероятность их появления описывается нормальным (Гауссовым) распределением P(y):

В этом случае наиболее вероятное значение у = у_ср, а вероятность попадания результатов измерения в заданные пределы составляет Р(у_ср ±σ_у) = 68,27 %,

Р(у_ср ±2σ_у)= 95,45% и Р(у_ср ±3σ_у) = 99,73 %.

Случайная погрешность также бывает абсолютной, относительной и приведенной. В частности, относительная средняя квадратическая погрешность ε_у = σ_у /у_ном (в расчетах у_ном приравнивают математическому ожиданию, т. е. принимают у_ном = у_ср). Использование дисперсионных оценок позволяет суммировать статистически независимые погрешности для любых законов распределения.

Для определения случайной погрешности иногда применяют квантильные оценки. Квантильная оценка — это указание максимального значения случайной погрешности (ε_v)_max с некоторой доверительной вероятностью Р(у). Общепринятые доверительные вероятности:

Р(у) = 0,80 — в стандартах надежности средств электроники, автоматики и измерительной техники;

Р(у) = 0,9...0,95 — при нормировании случайных погрешностей средств измерения.

Основной недостаток оценки погрешности доверительной вероятностью - невозможность суммирования погрешностей нескольких датчиков.

В соответствии с ГОСТ 8.011-72 при проведении метрологической по­верки датчика необходимо указывать закон распределения погрешностей. В ряде случаев близкие по форме законы могут быть приведены к одному виду.

Законы распределения подразделяют по трем основным признакам:

1) по форме кривой распределения — симметричные (нормальный, тре­угольный и др.) и скошенные;

2) по числу максимумов на кривой распределения — безмодальные, од­номодальные и двухмодальные;

3) по способу аналитического описания: экстремальные (в частности, дискретное двузначное распределение), симметричные экспоненциальные, композиционные и частные (например, арксинусоидальный).

Укажем для типовых погрешностей законы распределения (рис. 1.8):

погрешность от зазора в кинематической цепи распределена по дискретному двузначному закону, так как принимает только два значения: + а и - а (см. рис. 1.8, а);

погрешность от гистерезиса имеет композиционное распределение в ви­де суммы дискретного двузначного и экспоненциального законов, а также размытость около точек + аи-а (см. рис. 1.8, б);

погрешность от квантования распределена по равномерному закону, так как значения у>bиу<-b не встречаются, а внутри этого интервала они равновероятны (см. рис. 1.8, в);

погрешность от синусоидальной наводки распределена по арксинуидальному закону;

погрешность градуировки имеет композиционное распределение в виде суммы равномерного и экспоненциального законов;

температурная погрешность имеет композиционное распределение в виде суммы треугольного асимметричного и дискретного двузначного законов;

погрешность от колебаний напряжения питания распределена по тре­угольному закону.

Закон распределения погрешности для электронных систем общепро­мышленного назначения обычно известен. Например, шумы радиоаппарату­ры подчинены нормальному закону распределения (см. рис. 1.8, г).

Применение рассмотренных выше характеристик для оценки точности датчика предполагает составление паспорта датчика. Иногда для этого удобнее использовать интегральные оценки: постоянство, правильность и точность датчика.

Постоянство датчика — это такое его свойство, для которого характерна малая случайная погрешность (рис. 1.9, а). В этом случае обеспечивается высокая сходимость результатов измерений.

Правильностью (рис. 1.9, б) называется способность датчика выдавать результат с малой систематической погрешностью. (Наиболее вероятное значение измеряемой величины близко к истинному.)

Точность обозначает способность датчика выдавать результаты, индиви­дуально близкие к истинному значению измеряемой величины. Высокие постоянство и правильность датчика (рис. 1.9, в) обеспечиваются одновременно. Точность численно выражается через сумму случайной и систематической составляющих полной погрешности. Она определяет доверительный интервал вокруг измеренного значения, внутри которого с заданной вероятностью находится истинное значение измеряемой величины.

В заключение сформулируем основные требования, которые следует со-блюдать при разработке датчиков робототехнических и мехатронных систем.

1. Выделить измеряемый параметр и выбрать методику его измерения.

2. Разработать структуру информационных модулей, максимально используя симметричные и дифференциальные схемы.

3. Определить влияющие факторы и сформировать рабочие условия функционирования датчика.

4. Провести градуировку датчика и определить его функцию преобразования.

5. Вычислить относительную систематическую погрешность датчика.

6. Провести серию испытаний и установить закон распределения случайной погрешности: вычислить математическое ожидание и дисперсию случайной погрешности; определить относительную случайную погрешность датчика.

7. Рассчитать полную погрешность датчика и указать доверительный интервал.

8. Составить паспорт на датчик.

Контрольные вопросы

1. Как определить полосу пропускания датчика?

2. Можно ли установить реальную функцию преобразования датчика?

3. Зависит ли динамическая чувствительность датчика от статической?

4. Обладает ли датчик первого порядка собственной частотой?

5. Какой параметр характеризует быстродействие датчика?

6. От каких параметров зависит собственная частота датчика второго порядка?

7. Какую погрешность — аддитивную или мультипликативную — вызывают климатические факторы?

8. Можно ли случайную погрешность сделать систематической?

9. В чем основное достоинство дисперсионных оценок?

10. Как связаны между собой средние квадратические погрешности при единичном измерении и при нескольких измерениях?

---

Дата добавления: 2015-08-26