Датчики и их характеристики

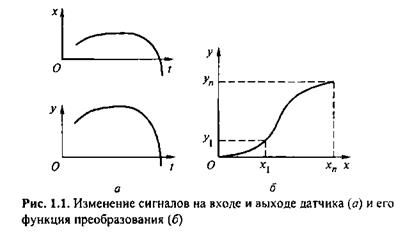
Датчик (измерительный преобразователь) — это устройство, обеспечи­вающее функциональное преобразование одной величины в другую величи­ну, участвующую в некотором информационном процессе. Рассматривая физические процессы в преобразователях, можно установить связь между выходным у и входным x сигналами (рис. 1.1, а), изменяющимися во време­ни:

Математическое (или графическое) описание этой связи называется функцией преобразования датчика (рис. 1.1, б). В большинстве случаев ин­формационные характеристики датчиков, в том числе их функцию преобра­зования, определяют на основании анализа преобразования сигналов в сис­теме.

Для датчиков с линейной функцией преобразования используют коэф­фициент преобразования:

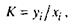
где x_i,у_j— текущие значения x и у.

В зависимости от числа измеряемых параметров датчик характеризуется одномерной или векторной функцией преобразования (например, одноком­понентный датчик силы и силомоментный датчик). Датчик, имеющий век­торную функцию преобразования

Y = F(Х), является многокомпонентным.

В принципе любой датчик можно считать многокомпонентным, по­скольку на него кроме измеряемой величины действуют факторы, обуслов­ленные внешними причинами. Тем не менее под многокомпонентным дат­чиком будем понимать только такой преобразователь, который конструк­тивно предназначен для измерения нескольких параметров. Особенностью многокомпонентного датчика является взаимное влияние каналов измере­ний. Для оценки этого свойства измерителя используют понятие «избира­тельность канала».

Пусть на входах n-канальной измерительной системы действует сигнал вызывающий некоторые сигналы на всех выходах системы. Тогда изби­рательностью к-го канала измерительной системы называется выражение вида

где у_к — сигнал на выходе k-го канала системы.

Для линейных систем избирательность характеризуется коэффициентом

влияния Ʌⁱ_j каналов:

где у_i, у_j— сигналы на выходах i-го j-го каналов; х_j — входное воздей­ствие на у-й канал. В частном случае при отсутствии влияния каналов Ʌⁱ_j = 0 и у_i - 0, т. е. на выходе канала образуется сигнал, пропорциональ­ный только измеряемой величине.

Если функции изменения во времени сигналов на входе и выходе диф­ференцируемы, то чувствительность датчика S = dy/dx. Чувствительность — важнейшая характеристика датчика, позволяющая оценить выходной сигнал по пределам изменения измеряемой величины и выбрать датчик, от­вечающий требованиям измерения. Для линейных преобразователей S = К и у = Кх = Sx, причем единицы измерения К и S одинаковы, например вольт на ньютон (В/Н). В общем случае чувствительность зависит от внешних факто­ров: напряжения питания, температуры, а также спектра и частоты измеряе­мого воздействия. Например, в паспорте на дифференциальный трансфор­матор TION фирмы Ifelec (Франция) указывается его чувствительность S₁ = 1,5 мВ/мм при частоте напряжения питания 50 Гц и S₂= 17 мВ/мм при 400 Гц.

Чувствительность датчиков определяют в статическом и динамическом режимах работы. Статическую чувствительность датчика S_c измеряют на основании его статической функции преобразования, причем S_c = К и сов­падает с S в том случае, если эта функция является прямой, проходящей через начало координат.

Динамическую чувствительность S_Д можно определить лишь в случае, когда измеряемая величина х является периодической функцией и выходной сигнал у имеет ту же периодичность, что и х. Например, если x(t) = x₀ + x₁cos ωt, то y(t) = у₀ + y₁ cos(ωt + ψ), где ω — круговая частота, ω= 2πƒ; ƒ— частота входного сигнала, Гц.

Обычно измеряемый сигнал не является гармонической функцией и сложным образом изменяется во времени. Если функцию x(t) разложить в ряд Фурье, то выходной сигнал у(t) будет представлять собой суперпозицию различных составляющих y_n(t):

Здесь у₀ — координата, определяющая рабочую точку на статической гра­дуировочной характеристике; ψ — сдвиг фаз между сигналами на входе и выходе.

Зависимость динамической чувствительности от частоты ƒ представ­ляет собой частотную характеристику датчика. Функция S_a (ƒ) зависит от

механической, тепловой и электрической инерции преобразователя, т. е. его массы т, электрического сопротивления R, индуктивности L и емкости С. Частотные характеристики датчика определяются порядком дифференци­ального уравнения, описывающего его конструктивную схему. В соответст­вии с этим выделяют датчики первого и второго порядка.

Датчики первого порядка в своей структуре не содержат колеблющихся частей. К ним относятся, например, оптические преобразователи — свето- и фотодиоды. Функция преобразования датчика первого порядка описывается дифференциальным уравнением первого порядка

где А и B – константы. В комплексной форме

и функция преобразования датчика первого порядка принимает вид

Где x₁,y₁ – действительные величины. Представляя граничную частоту в виде

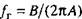, а сдвиг фазы как

ваываываывввв

,получаем

Таким образом, частотная характеристика датчика первого порядка определяется зависимостью

,или

где S(0) = 1/В. В частном случае при ƒ <<ƒ_г S(ƒ) = S(0). Вид амплитудно- частотных (АЧХ) и фазочастотных характеристик (ФЧХ) представлен на рис. 1.2, а.

Датчики второго порядка (например, пьезоэлектрические акселеромет­ры) содержат в своей структуре колеблющиеся элементы и характеризуются собственной частотой ƒ₀ и коэффициентом затухания ζ. Функция преобразования датчика представляет собой дифференциальное уравнение вида

а частотная характеристика определяется зависимостью

Принято считать, что оптимальное значение коэффициента затухания ζ ле­жит в пределах 0,6...0,7. Частотные характеристики датчика второго порядка представлены на рис. 1.2, 6

Полоса пропускания В датчика — это диапазон частот, в котором орди­наты АЧХ уменьшаются относительно их максимального значения не более чем н а 3 дБ. В расчетах можно считать, что полоса пропускания соответст­вует горизонтальному участку АЧХ. Для датчиков первого порядка имеем 20 lg S(ƒ_r)/S(0)= 3 дБ, т. е. В=ƒ_г. Ширина полосы пропускания датчиков второго порядка зависит от С,. При ζ = 0,6...0,7 полоса пропускания В =ƒ_г.

Датчик называется линейным в некотором диапазоне измеряемой вели­чины, если его чувствительность не зависит от значения этой величины. В линейном диапазоне выходной сигнал пропорционален измеряемому пара­метру, причем в статическом режиме

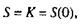
в динамическом для датчиков первого и второго порядка соответственно имеем

Итак, в динамическом режиме линейность датчика зависит от чувстви­тельности в статическом режиме S(0) и от параметров частотной характери­стики (ƒ_г, ƒ₀, ζ). В частном случае, когда датчик работает только в динами­ческом режиме (это характерно, например, для акустического дальномера), S(0) = 0.

На практике линейность датчика определяют по его градуировочной ха­рактеристике. Эту характеристику снимают экспериментальным путем, причем распределение экспериментальных данных аппроксимируют урав­нением некоторой прямой, используя метод наименьших квадратов. Напом­ним, что в этом случае средняя сумма квадратов отклонений эксперимен­тальных точек от полученной прямой минимальна.

Установлено, что приближение экспериментальной зависимости к пря­мой вида у = ах + b достигается при

где N — число точек аппроксимации.

Поведение датчика в установившемся режиме описывает его АЧХ, тогда как на переходных режимах оно определяется инерционными свойствами датчика. Характер переходного режима не зависит от закона изменения из­меряемой величины, а определяется только свойствами элементов собствен­но датчика. Быстродействие — это параметр датчика, позволяющий оценить как выходной сигнал следует во времени за изменением измеряемой величины. Таким образом, быстродействие характеризует время, необходи­мое для того, чтобы влияние переходных процессов на выходную величину стало пренебрежимо малым для заданной точности. Параметр, используе­мый для количественного описания быстродействия, называется временем установления t_уст. Следовательно, (t_уст — это интервал времени, который должен пройти после приложения ступенчатого сигнала, для того чтобы сигнал на выходе датчика достиг уровня, отличающегося от входного не более чем на заданную величину ε. Различают четыре составляющие времени установления t_уст (рис. 1.3):

· время задержки нарастания t_зн — время, соответствующее увеличению выходного сигнала на 10 % от установившегося значения;

· время нарастания ƒ_н — время, необходимое для увеличения выходного сигнала от 10 до 90 % от установившегося значения;

· время задержки спада ƒ_зс — время, соответствующее умень­шению выходного сигнала на 10 % от установившегося значе­ния;

· время спада t_с — время, тре­буемое для уменьшения выходно­го сигнала от 90 до 10 % от уста­новившегося значения.

Поскольку уравнение динами­ки датчиков

первого порядка в переходном режиме имеет вид

то при начальных условиях(y=0,t=0)

где y₀=x₀/B, τ=A/B=1/(2π𝑓_г) –установившееся значение выходного сигнала и постоянная времени датчика соответственно.

время установления t_уст можно определить по графику переходного

процесса (рис. 1.4, а). При этом необходимо указывать ошибку г между те­кущим значением у и его установившимся значением у₀: ε = (у₀ - у)/у₀. Так,

для ε = 1 % t_уст = 4,6τ = 0,73/ƒ_г, для ε = 10 % t_уст ≈t_H = t_c = 2,3τ. Следова­тельно, чем выше граничная частота, тем выше быстродействие датчика.

Уравнение динамики датчика второго порядка в переходном режиме имеет вид

Часто при оценке переходных процессов наряду с коэффициентом зату­хания ζ используют понятие «декремент затухания». Декремент затухания δ — это величина, обратная числу колебаний, по окончании которых макси­мальное значение амплитуды убывает в е раз (где е — основание натураль­ных логарифмов, е ≈ 2,718):

От быстродействия следует отличать производительность устройства (обычно характерна для цифровых систем), определяемую числом операций в секунду. На быстродействие датчика влияют факторы, не связанные с ним непосредственно, например окружающая среда. Так, для резистивного тер­мометрического зонда при ε=10%t _уст составляет 2,6 с в воде, текущей со скоростью 0,2 м/с, и 40 с в воздухе, движущемся со скоростью 1 м/с. Тре­бования к чувствительности и быстродействию датчика противоречивы, по­этому при расчетах это необходимо учитывать.

Дата добавления: 2015-08-26