ПРИМЕРЫ. 10.1. Определить давление центробежного насоса системы охлаж­

10.1. Определить давление центробежного насоса системы охлаж­

дения двигателя, при котором его подача Q= 12 л/с, если диаметр рабочего

колеса D₂=180 мм частота вращения п = 3200 мин-1, ширина канала рабочего

колеса на выходе b_z = 10 мм, средний диа­метр окружности, на которой расположены входные кромки лопастей, D₁=60 мм количество лопастей их толщина, выходной угол лопастей (рис. 10.2). Объемный КПД насоса гидравлический Считать, что поток воды подводится к лопастям р адиально

Решение.

Определяем меридиональную составляющую абсолютной скорости на выходе из выражения(10.1)для подачи насоса

Окружная скорость на выходе

Проекция абсолютной скорости на окружную скорость

Коэффициент влияния числа лопастей

Напор насоса определяем по формуле (10.5):

Давление, развиваемое насосом.

10.2. Рабочее колесо центробежного насоса, вращающееся с час­тотой n = 1450 мин^-1, имеет следующие размеры (рис. 10.2); диа­метр внешней окружности D₂ = 150 мм, средний диаметр окружности, на которой расположены входные кромки лопастей, D₁ = 50 мм, ши­рина канала рабочего колеса на входе b₁ = 15 мм, на выходе — b₂ = — 12 мм, входной угол лопастей 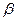= 60°, выходной угол 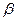₂ = 20°. Количество лопастей z = 6, их толщина = 4 мм, объемный КПД насоса 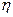0 = 0,95, гидравлический — 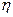r = 0,90, коэффициент влияния числа лопастей k_z = 0,78..

При какой подаче абсолютная скорость жидкости на входе в ра­бочее колесо будет направлена по радиусу? Каким будет при этом, напор насоса? Считать, что скорость относительного движения направ­лена по касательной к лопасти.

Решение. При радиальном подходе жидкости угол аг (рис. 10.2) между абсолютной скоростью v1 и окружной скоростью их равен 90°, причем

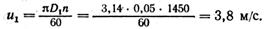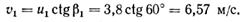Из параллелограмма скоростей на входе в рабочее колесо находим абсолютную скорость

Коэффициент стеснения потока на выходе

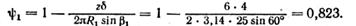Подача насоса (в данном случае v_м1=v₁)

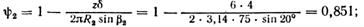Для определения напора насоса найдем сначала коэффициент стеснения потока и меридиональную составляющую скорости на выходе:

Окружная скорость на выходе из рабочего колеса

Проекция абсолютной скорости на окружную

Напор насоса

10.2. Подобие лопастных насосов. Расширение области применения центробежных насосов обточкой рабочих колес

Теоретические решения многих вопросов, связанных с движением вязких жидкостей в проточной части насосов, еще не найдены. При конструировании и изготовлении новых образцов насосов неясные во­просы отрабатываются на модели. Полученные на модели зависимости переносятся затем на натурную машину по законам гидродинамиче­ского подобия. На основании этих законов производится также пере­счет характеристик насоса на другие частоты вращения.

Исходя из общих законов гидродинамического подобия, гидрома­шины можно считать подобными, если будет соблюдаться геометри­ческое, кинематическое и динамическое подобие. Центробежные на­сосы обычно работают при больших значениях чисел Рейнольдса, т. е. в области автомодельности, когда для гидродинамического подобия достаточно лишь геометрического и кинематического подобия.

Кинематическое подобие выражается в подобии параллелограммов скоростей в любых сходственных точках натуры и модели (рис. 10.4), из которого следует, что

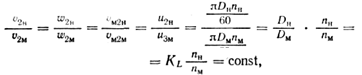где — масштаб геометрического подобия — число, показывающее, во сколько раз геометрические размеры в натуре отличаются от соответствующих размеров в модели; и — соответственно частота вращения рабочего колеса в натуре и в модели.

Найдем отношения подач, напоров и мощностей подобных насосов, принимая во внимание-то, что объемные, гидравлические и полные КПД в натуре и модели примерно одинаковы,

и используя формулы (10.1), (10.4) и (10.7):

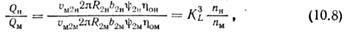Так как коэффициенты стеснения для геометрически подобных асосов одинаковы;

так как для подобных насосов коэффициенты одинаковы;

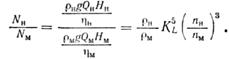
Для двух одинаковых насосов (K_L = 1), работающих с различной частотой вращения и перекачивающих жидкость той же плотности, законы подобия (10.8) — (10.10) принимают вид

(10.11)

Зависимости (10.11) обычно называют законами пропорциональ­ности центробежных насосов. По ним производится пересчет рабочих характеристик насоса на другую частоту вращения. Рассмотрим кон­кретный пример. Пусть рабочая характеристика насоса при частоте вращения п₁ задана в 10.1.

Пересчитаем ее на частоту вращения n₂ = 0,9n₁ На основании формул (10.11) находим:

Следовательно, для получения харак­теристики насоса при частоте вращения п₂ необходимо первую строку табл. 10.1 умножить на 0,9, а вторую — на 0,81. КПД для подобных режимов принимаются одинаковыми. В результате выполнения указанных расчетов получаем характе­ристику насоса при частоте вращения n₂(табл. 10.2).

Пусть заданы характеристики насоса при частотах вращения n₁ и n₂ (рис. 10.5). Покажем, что подобные режимы, определя­емые точками 1 и 2, лежат на квадратичной

таблица 10.2

параболе, проходящей через начало координат. Для этого подставим в отношения напоров

значение .В результате

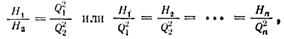
В результате получаем

или

Это и есть уравнение параболы подобных режимов (штриховая линия на рис. 10.5). Законы пропорциональности (10.11) справедливы только для точек, лежащих на этой кривой.

Критерием подобия центробежных насосов является коэффициент быстроходности

(10.12)

Формула (10.12) для определения коэффициента быстроходности выводится из формул (10.8) и (10.9) путем исключения из них вели­чины Kl. Он вычисляется для оптимального режима работы насоса

()Коэффициент быстроходности характеризует способность насоса создавать напор («напороспособность») и обеспечивать подачу («подачеспособность»). Чем больше n_s, тем меньше «напороспособность» и больше «подачеспособность»

насоса.

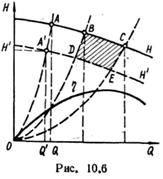
Если двигатель насоса нерегулируемый, а от насоса требуется по­лучить режим работы, соответствующий точке А' с координатами Q'H’, которая не лежит на характеристике насоса (рис. 10.6), то применяют обточку рабочего колеса по наружному диаметру. При этом кривая Н = f (Q) опускается вниз и при некотором значении диаметра D' пройдет через заданную режимную точ­ку A'.

Для расчета характеристики насоса, получающейся после обточки рабочего коле­са, применяются эмпирические формулы

(10.13)

в которых D, Q и Н — соответственно наружный диаметр, подача и напор насоса с необточенным рабочим колесом; D', Q' и Н' — то же для насоса с обточенным рабочим колесом. Из уравнений (10.13) следует, что

Следовательно, режимы А и А', удовлетворяющие уравнениям (10.13), лежат на квадратичной параболе, которую называют пара­болой обточек.

Допустимая величина обточки рабочего колеса выбирается в зависимости от коэффициента быстроходности насоса:

Насос целесообразно эксплуатировать только в области высоких КПД (участок ВС на рис. 10.6). Криволинейный четырехугольник BCED, ограниченный характеристиками насоса с необточенным ра­бочим колесом (крива H = f (Q)) и с максимально обточенным рабо­чим колесом (кривая H' = f (Q)) и параболами обточек, проходящими через точки В и С, называют рабочим полем насоса. Режимы, лежащие в пределах этого четырехугольника, являются рабочими.

Для выбора центробежного насоса по заданным значениям напора Н и подачи Q используется сводный график рабочих полей насосов (прил. 8).

Дата добавления: 2015-08-26