Методические рекомендации по выполнению контрольной работы.

При решении задачи №1 необходимо, в первую очередь, определить единицу изучаемого множества, её первичные и вторичные признаки. По первичным признакам расчёт общей средней выполняется по схеме простой арифметической. Для вторичного признака определяем схему расчёта его индивидуальных значений и выражаем неизвестный признак через известные, используя их буквенные обозначения. Полученную расчётную схему применяем для определения общей средней.

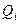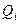Например, по условию задачи по нескольким предприятиям известна стоимость продукции - и выработка продукции на 1-го работника - . Так как признак является первичным, значение его общей средней рассчитаем по простой арифметической: .

Признак - вторичный, его индивидуальные значения получены по формуле:

Стоимость продукции: Численность работников. Численность работников по условию неизвестна, но её можно найти, если выразить через Стоимость продукции и Выработку на 1-го работника, то есть, Численность работников = . Тогда общая средняя будет рассчитана следующим образом: . Здесь использована средняя гармоническая взвешенная, а весом является первичный признак 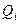- Стоимость продукции. Следует помнить, что весом всегда выступает первичный признак, в какой бы сложной форме он ни присутствовал в используемом расчёте.

При решении задачи №2 необходимо определить границы «открытых» интервалов, применяя величину интервала 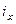, которая для всех групп остаётся одинаковой. Далее выполняется расчёт серединного значения признака в каждом интервале как полусуммы его максимального и минимального значений: 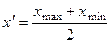. Расчёт показателей вариации основан на использовании формул для вариационного ряда, то есть, в расчёте участвуют частоты - . Необходимо рассчитать среднее значение признака - , среднее квадратическое отклонение - , коэффициент вариации - , коэффициент асимметрии - , значение моды - Здесь - центральный момент третьего порядка; . Вариационный ряд иллюстрируют полигон распределения частот и гистограмма. При построении полигона ломаная линия должна пересечь ось ОХ в серединах «нулевого» интервала и «К+1» интервалов, каждый из которых имеют нулевые частоты: , иначе площади полигона и гистограммы не будут равны.

В задаче №3 предполагается выполнить расчёт абсолютных и относительных (нормированных) показателей различий 2-х структур. Средний арифметический показатель определяется по формуле: 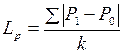. Здесь и - показатели удельного веса, оценивающие отчётную и базисную структуры и выраженные в процентах: . Показатель определяет на сколько процентных пунктов в среднем отличается удельный вес каждой группы отчётной и базисной структуры. Относительная или нормированная оценка показывает сколько процентов составляют фактические различия двух структур от величины их предельных различий, составляющих 200%: процентов.

Коэффициент Гатева принадлежит к группе квадратических нормированных характеристик и показывает сколько процентов составляют фактические различия 2-х структур от их возможных различий: 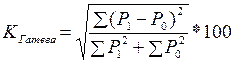(процентов). Различия дух структур иллюстрируются столбиковой диаграммой, в которой рассматриваются фигуры, образовавшиеся в «зоне перехода» от одной структуры к другой.

Решение задачи №4 начинается с выяснения природы изучаемых явлений: относятся они к категории соизмеримых или несоизмеримых. Для несоизмеримых явлений характерна различная физическая форма и разное их потребительское назначение.

Затем анализируется связь признаков, значения которых приведены в условии задачи. При использовании индексов обычно предполагается наличие жёсткой мультипликативной связи признака-результата и признаков-факторов: Например, зависимость товарооборота - от физического объёма реализованных товаров разного вида - и от цен за единицу товара каждого вида - . Следует определить, какой из признаков данной системы отсутствует в условии задачи и рассчитать его значения в базисном и отчётном периодах. Если, например, отсутствует , тогда ; если отсутствует , тогда ; если отсутствует , тогда .

Например, для оценки происшедших изменений признаков W, Q и P выберем систему индексов для анализа несоизмеримых явлений: систему индивидуальных индексов - и систему сводных (агрегатных) индексов - .

Расчёт сводного индекса признака-результата - W выполняется по схеме:

.

Например, 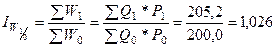или 102,6%.

Уровень товарооборота в отчётном периоде составил в среднем 102,6% от его уровня в базисном периоде, то есть он увеличился в среднем на 2,6% (1,026*100%-100%=2,6%), что составило 5,2 млн руб. (205,2-200,0=5,2 млн руб.).

Сводный индекс первичного признака-фактора Q рассчитаем по схеме:

.

Следует выполнить расчёт W_{условное} = Q₁*P₀. и определить величину .

В нашем примере: 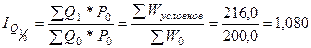или 108,0%. Уровень отчётных значений физического объёма продаж – составил от уровня его базисных значений в среднем 108%. Физический объём - за отчётный период увеличился в среднем на 8%, это привело к увеличению значений товарооборота - W на 16 млн руб.

Сводный индекс вторичного признака-фактора P рассчитаем по схеме:

.

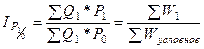В нашем примере: или 95,0%. Уровень цен - на товары разного видав отчётном периоде составил в среднем 95% от уровня их значений в базисном периоде, то есть цены - за отчётный период уменьшились в среднем 5%, это привело к уменьшению значений товарооборота - W на 10,8 тыс руб.

Представим результаты в виде системы индексов в относительной форме:

или

1,026 = 1,080 * 0,950.

Из двух факторов, влияющих на результат, один изменился в большей мере: на + 8% ( или 8% прироста), а другой – в меньшей степени: на –5% ( или 95%, то есть прирост составил – 5%).

Представим в виде системы величину абсолютных размеров прироста результата за счёт каждого фактора: или

+ 5,2 млн руб. = + 16,0 млн руб. + (–10,8) млн руб.

В нашем примере, в результате увеличения физического объёма продаж товарооборот увеличился на 16,0 млн руб., а за счёт снижения цен товарооборот уменьшился на 10,8 млн руб. В целом же, совместное влияние обоих факторов привело к увеличению товарооборота на 5,2 млн руб.; это было вызвано более сильным воздействием возросшего физического объёма продаж.

Решение задачи №5 начинается с выяснения природы изучаемых явлений: относятся они к категории соизмеримых или несоизмеримых. Соизмеримые явления характеризуются одинаковой физической формой и одинаковыми потребительскими свойствами, назначением и использованием. Например, необходимо изучить зависимость и изменения значений признаков: W –стоимость произведённой продукции; T – численность работников; S – выработка продукции в среднем на 1-го работника. Зависимость признаков выражается соотношением: W_i = T_i * S_i.

Отсутствующие в условии задачи значения признаков у изучаемых единиц множества необходимо рассчитать: неизвестные значения W_i = T_i * S_i; неизвестные значения ; неизвестные значения .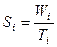

Для анализа соизмеримых явлений используются система сводных индексов:

.

В условии задачи предлагается рассмотреть ту часть системы, где более подробно анализируются факторы изменения среднего значения вторичного признака и рассчитать индекс переменного состава - , индекс постоянного состава - 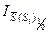и индекс структурных сдвигов - 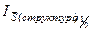, то есть систему сводных индексов в относительной форме:

.

Для расчёта указанных индексов необходимы значения общей средней выработки, которые определяются по формуле: .

Индекс переменного состава или индекс общей средней рассчитаем по схеме:

.

Пусть в нашем примере (тыс руб.); (тыс руб.), тогда или 107,0%. Общая средняя выработка отчётного периода оставила от уровня базисного периода 107%, то есть средняя выработка возросла на 7%

Индекс постоянного состава или индекс собственно выработки покажет как изменилась общая средняя под влиянием изменений индивидуальных значений вторичного признака; его значение определим по схеме:

.

В расчёте участвует условная средняя выработка, значение которой определяется на основе условной величины результата – условной стоимости продукции; её необходимо предварительно рассчитать.

В нашем примере

(тыс руб.). Тогда: или 104,3%.

Индекс постоянного состава показывает, что в результате изменения индивидуальной выработки работников общая средняя выработка в отчётном периоде составила 104,3%, то есть возросла на 4,3%.

Индекс структурных сдвигов оценивает изменения общей средней под влиянием изменений удельного веса единиц с высокими и низкими значениями вторичного признака-фактора.

или 102,6%.

В результате увеличения удельного веса работников с высоким уровнем выработки и уменьшения удельного веса работников с низким уровнем общая средняя выработка составила 102,6% от базисного уровня, то есть возросла на 2,6%. Если бы в структуре произошли противоположные изменения, тогда бы общая средняя уменьшилась, а величина индекса структуры была бы меньше единицы.

Представим полученные результаты в виде системы индексов в относительной форме:

; в нашем примере 1,070 = 1,043 * 1,026.

Увеличение общей средней выработки на 7% произошло в результате увеличения индивидуальной выработки на 4,3% и на 2,6% за счёт изменений в структуре работников. Из двух факторов, повлиявших на увеличение общей средней выработки, изменения индивидуальной выработки были более значительными, а их влияние на увеличение общей средней - более сильным, чем влияние изменений в структуре работников.

При решении задачи 6 необходимо по информации об изменениях цен по товарным группам рассчитать общий индекс цен, используя схемы Пааше и Ласпейреса.

Расчёт общего индекса цен Пааше и Ласпейреса выполняется по следующим формулам: ; .

Для их расчёта по условию задачи необходимо использовать форму сводного индекса как среднего из индивидуальных, применяя либо гармоническую взвешенную, либо арифметическую взвешенную. В первом случае весом выступают отчётные значения признака-результата – W₁. В другом случае, весом выступают базисные значения признака-результата – W_0.

В расчёте сводного индекса цен Пааше участвует отчётная информация о структуре потребления, в которой нашла отражение склонность населения к потреблению более дешёвых товаров и тех, на которые цены снизились в меньшей степени. То есть в индексе Пааше учтена эластичность потребительского рынка.

.

Индекс Ласпейреса получен как средний арифметический из индивидуальных индексов цен, скорректированных на базисную структуру признака-результата. Индекс цен Ласпейреса (в отличие от индекса цен Пааше) не учитывает эластичность потребительского рынка. Различия в значениях индексов цен Ласпейреса и Пааше, которые известны как эффект Гершенкрона, объясняются указанными особенностями их построения, в которых отражается разное отношение к учёту эффекта эластичности потребительского рынка.

В задача 7 необходимо сформировать случайную бесповторную выборку, рассчитать по ней значение средней () и доли (), их ошибки ( и ) и построить доверительный интервал ( и 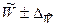) возможных значений генеральной средней и генеральной доли.

При формировании выборочного множества используют либо механический отбор, либо жеребьёвку, обычно применяя таблицу случайных чисел (ТСЧ). Механический отбор предполагает расчёт шага отбора - ; где - число единиц генерального множества; - число единиц выборочной совокупности. Порядковый номер первого элемента выбирается случайно, например, по ТСЧ. Если первый элемент выборки имеет номер = 7, то при h = 15 в выборку будут отобраны единицы с номерами 7, 22, 37, 52, 67 и т.д.

При использовании ТСЧ устанавливается и фиксируется в комментариях правило, по которому будут отбираться пятизначные числа и их используемые разряды. Например, отбираем числа, двигаясь слева направо по строке, начиная с ячейки первой графы первой строки. Из выбранных 5-тизначных чисел используем первую и вторую цифры. В Приложении дана таблица случайных чисел (таблица 2. По указанному правилу производим отбор чисел и их цифр: 66 194, 28 926, 99547, 16 625, 45 515, 67 953, 78240, 43 195, 24 837, 32 511, 00833, 88000, 67299, 68 215, 11 274. Если генеральное множество содержит, например, 70 единиц, то номера 99547, 78240, 00833 не используются. Если выборка бесповторная, то раз отобранная единица, например, с номером 67 (67 953), в дальнейшем отборе не участвует.

Из таблицы исходных данных выписываем значения изучаемого признака у единиц, отобранных в выборку. Например, при изучении среднедушевых расходов населения РФ отобраны 10 заводов с указанными номерами и по ним собраны сведения о сумме ежемесячных среднедушевых расходов населения, тыс. руб.

N														, %
п/п
X	12,82	1,40	1,59	1,48	1,22	1,14	1,59	2,26	2,65	1,83	27,98	2,798	3,37
n’	—	+	+	+	+	+	+	—	—	+		х	х	х

Рассчитаем =2,798 тыс руб., 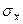=3,37 тыс руб., число заводов n’ =7, где расходы меньше среднедушевых ежемесячных ресурсов семьи, которые составляют 2,17 тыс. руб., и их долю =0,70.

Определим значения средних возможных ошибок средней и доли:

(тыс руб.);

или 13,5%.

С вероятностью P=0,972 определим величину предельных ошибок средней и доли. Для P=0,972 коэффициент доверия t =2,2.

Тогда (тыс руб.); или 29,7%.

Определим границы доверительного интервала возможных значений генеральной средней - 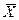и генеральной доли .

Границы значений генеральной средней: = 2,798 . С вероятностью 97,2% можно утверждать, что уровень среднемесячных душевых расходов населения РФ находится в интервале от 0,609 до 4,987 тыс. руб. Возможные значения генеральной средней располагаются в достаточно широких границах, это указывает на невысокую точность выводов. Но при этом высока надёжность границ, так как они позволяют оценить значение генеральной средней по результатам 97,2% всех возможных выборок данного объёма.

Значение генеральной доли будет находится в интервале: . С вероятностью 97,2% можно утверждать, что доля заводов, где расходы меньше средних ресурсов семьи будет находиться в интервале от 40,3% до 99,7%. Границы доверительного интервала также достаточно широкие, но они сочетаются с высокой вероятностью отражения значения генеральной доли. Основная причина широких границ доверительного интервала в том, что значения величины расходов – X характеризуются чрезвычайно высокой вариацией (), которая объясняется присутствием в выборке территории с порядковым номером 11 (г.Москва; X₁₁ = 12,82 тыс руб.), для которой характерно аномально высокое значение изучаемого признака. В том случае, если бы состав объектов выборки сформировался иначе и указанная территория в выборку не попала, результаты были бы точнее.

Решение задачи 8 предполагает изучение корреляционной связи двух переменных методом наименьших квадратов (МНК). Покажем порядок решения на примере данных за 2000 год по территориям Северо-Западного федерального округа

Предварительное представление об изучаемой связи даёт исходное множество заводов, ранжированное по значению фактора – X, а также график зависимости результата – Y от фактора – X. Для построения графика расположим территории по возрастанию значений фактора . По графику сделаем вывод о наличии линейной связи результата – Y с фактором – X. См. табл. 1.

Для отображения линейной формы связи переменных построим уравнения прямой: . Расчёт неизвестных параметров и выполняется методом наименьших квадратов (МНК), решая систему нормальных уравнений с использованием определителей второго порядка Δ, Δа₀ и Δа_1. Расчётные процедуры оформляются в разработочной таблице. См. табл.2.

Таблица 1.

Территории Северо-Западного федерального округа	Общая сумма доходов населения за год, млрд. руб.	Оборот розничной торговли за год, млрд. руб.
А
1. Псковская обл.	11,6	7,3
2. Новгородская обл.	14,8	9,3
3. Калининградская обл.	19,0	14,0
4. Респ. Карелия	19,1	9,4
5. Ленинградская обл.	26,2	15,6
6. Вологодская обл.	27,5	12,1
7. Архангельская обл.	30,0	16,3
8. Респ. Коми	37,3	16,7
9. Мурманская обл.	39,5	20,5
Итого	225,0	121,2
Средняя	25,0	13,47
	9,120	4,036
Дисперсия, D	83,182	16,289

Таблица 2

№
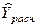
А
	11,6	7,3	134,6	84,7	8,1	-0,8	5,9
	14,8	9,3	219,0	137,6	9,4	-0,1	0,7
	19,0	14,0	361,0	266,0	11,1	2,9	21,5
	19,1	9,4	364,8	179,5	11,1	-1,7	12,6
	26,2	15,6	686,4	408,7	13,9	1,7	12,6
	27,5	12,1	756,3	332,8	14,5	-2,4	17,8
	30,0	16,3	900,0	489,0	15,5	0,8	5,9
	37,3	16,7	1391,3	622,9	18,4	-1,7	12,6
	39,5	20,5	1560,3	809,8	19,3	1,2	8,9
Итого	225,0	121,2	6373,6	3331,0	121,2	0,0	98,5
Средняя	25,0	13,5	—	—	—	—	10,9
Сигма	9,12	4,04	—	—	—	—	—
Дисперсия, D	83,18	16,29	—	—	—	—	—
Δ=	6737,76	—	—	—	—	—	—
Δа0=	23012,4		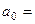3,415	—	—	—	—
Δа1=	2708,91		0,402	—	—	—	—

Расчёт определителей выполняется по следующим формулам:

Определитель системы 9*6373,6 – 225,0*225,0 = 6737,76;

Определитель свободного члена уравнения

= 121,2*6373,6 – 3331,0*225,0 = 23012,4.

Определитель коэффициента регрессии:

= 9*3331,0 – 121,2*225,0 = 2708,91.

Параметры уравнения регрессии имеют следующие значения:

; .

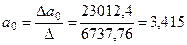Теоретическое уравнение регрессии следующего вида: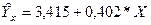

Коэффициент регрессии а₁ = 0,402 означает, что при увеличении доходов населения на 1 тыс. руб. (от своей средней) объём розничного товарооборота возрастёт на 0,402 млрд. руб. (от своей средней).

Свободный член уравнения а₀ = 3,415 оценивает влияние прочих факторов, оказывающих воздействие на объём розничного товарооборота.

Относительную оценку силы связи даёт общий (средний) коэффициент эластичности: . В нашем случае, когда рассматривается линейная зависимость, расчётная формула преобразуется к виду: 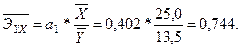Это означает, что при изменении общей суммы доходов населения на 1% от своей средней оборот розничной торговли увеличивается на 0,744 процента от своей средней.

Оценку тесноты связи дают линейный коэффициент парной корреляции и детерминации:

;

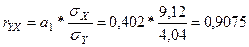Коэффициент корреляции, величина которого больше 0 и составляет 0,9075, показывает, что выявлена прямо пропорциональная, весьма тесная зависимость между общей суммой доходов населения за год и оборотом розничной торговли за год. Коэффициент детерминации, равный 0,824, устанавливает, что вариация оборота розничной торговли на 82,4% (из 100%) предопределена вариацией общей суммы доходов населения; роль прочих факторов, влияющих на розничный товарооборот, определяется в 17,6%, что является сравнительно небольшой величиной.

Дата добавления: 2015-08-20