
Читайте также:
|
АБЖ талдау және синтездеу үшін автоматикада дифференциалдық теңдеулерді қолданумен қатар кешенді айнымалы функцияларды және Лаплас түрлендіруін қолданады. Лаплас түрлендіруі күрделі дифференциалдық теңдеулерді алгебралық теңдеулерге алмастыру жолымен АБЖ есептерін шешуге мүмкіндік береді. Сонымен қатар, интегралдау тұрақтысын анықтау қажеттілігі жоғалады және кез келген біртекті емес дифференциалдық теңдеулердің жалпы шешімін тез анықтауға мүмкіндік пайда болады (2.1).
Дирихле шарты орындалған жағдайда, яғни f(t) функциясы t<0 кезінде нөлге тең болатын үздіксіз және дифференциалдаушы функция болған кезде, f(t) функциясының Лаплас түрлендіруі болатыны туралы жоғары математика курсынан белгілі.
f(t) функциясы түпнұсқа (оригинал) деп аталынады. Лаплас түрлендіруі келесі өрнекпен орындалады:
 .
.
мұндағы F(s) – f(t) функцияның бейнесі,  - кешенді айнымалы (Лаплас операторы).
- кешенді айнымалы (Лаплас операторы).
Кері Лаплас түрлендіруі келесі түрге ие:
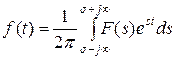 .
.
Бұл түрлендіру белгілі бейне бойынша түпнұсқаны (оригиналды) анықтауға мүмкіндік береді.
Тәжірибеде, әдетте, тура және кері Лаплас түрлендіруін орындау үшін 2.1 – кестеде келтірілген нәтижелер қолданылады.
Бұл жағдайда АБЖ түрлендіру операторы кешенді беріліс функциясы түрінде анықталады. Кешенді беріліс функциясы нөлдік бастапқы шартында Лаплас бойынша функциялар бейнелерінің қатынасы, яғни шығыс Y(s) және кіріс U(s) бейнелердің қатынасы ретінде анықталады
 (2.16)
(2.16)
Мұндағы (2.16)  ,
,  кешенді көпмүшелік. Оны (2.2) өрнектегі В(р) және А(р) оператолық көпмүшеліктерде p операторды s операторымен алмастыру арқылы анықтауға болады. 2.16 теңдеудің бөліміндегі сипаттама теңдеуінің түбірі полюстер деп аталынады. Сызықты жүйенің полюстері толығымен оның орнықтылығын анықтайды. Егер полюстердің нақты бөлігі теріс болса, онда жүйе орнықты болады. (2.16) теңдеудің алымындағы сипаттама теңдеуінің түбірлерін нөлдер деп атайды. Нөлдер экспоненциалды функцияның коэффициенттер мәнін анықтайды, бірақ орнықтылыққа әсер етпейді.
кешенді көпмүшелік. Оны (2.2) өрнектегі В(р) және А(р) оператолық көпмүшеліктерде p операторды s операторымен алмастыру арқылы анықтауға болады. 2.16 теңдеудің бөліміндегі сипаттама теңдеуінің түбірі полюстер деп аталынады. Сызықты жүйенің полюстері толығымен оның орнықтылығын анықтайды. Егер полюстердің нақты бөлігі теріс болса, онда жүйе орнықты болады. (2.16) теңдеудің алымындағы сипаттама теңдеуінің түбірлерін нөлдер деп атайды. Нөлдер экспоненциалды функцияның коэффициенттер мәнін анықтайды, бірақ орнықтылыққа әсер етпейді.
2.1 – кесте
Лаплас түрлендіруінің кейбір маңызды түрлері.
ƒ 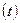
|  F F 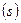
|
Қадамдық функция, u 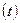
| 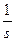
|
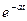
| 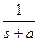
|
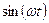
| 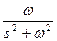
|
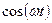
| 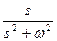
|
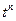
| 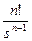
|
ƒ 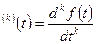
| 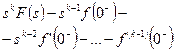
|
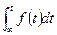
| 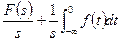
|
Импульстік функция, 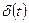
|
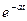 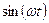
| 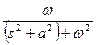
|
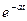 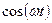
| 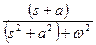
|
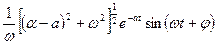 , , 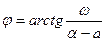
| 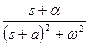
|
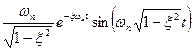 , , 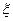 <1 <1
| 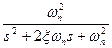
|
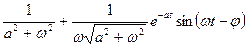 , , 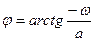
| 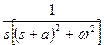
|
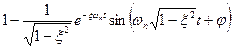 , , 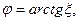 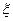 <1 <1
| 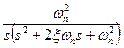
|
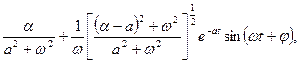 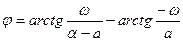
| 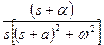
|
Дата добавления: 2015-08-20; просмотров: 1108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Басқарылыну және бақылану | | | Статикалық қасиеттерді бағалау |