
Читайте также:
|
Күй айнымалыларының п - өлшемді кеңістігінде жүйенің әр күйіне 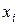 (i = 1, 2,... п) айнымалылар мәндерімен анықталатын бейнелейтін нүктенің қайсыбір орны сәйкес келеді.
(i = 1, 2,... п) айнымалылар мәндерімен анықталатын бейнелейтін нүктенің қайсыбір орны сәйкес келеді.
Айталық, күй кеңістігінде 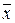 екі жиынтық
екі жиынтық 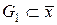 және
және  берілсін. Егер шектелген уақыт аралығында 0<t<T анықталған және бейнеленетін
берілсін. Егер шектелген уақыт аралығында 0<t<T анықталған және бейнеленетін 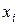 нүктені G1 аймағынан G2 аймағына ауыстыратын u=(u1,u2,…,ur)T басқару болса, онда қарастырылып отырған жүйе басқарылынатын болып келеді.
нүктені G1 аймағынан G2 аймағына ауыстыратын u=(u1,u2,…,ur)T басқару болса, онда қарастырылып отырған жүйе басқарылынатын болып келеді.
Егер шығыс координатаның векторын 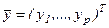 құрастыруда
құрастыруда 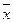 күй айнымалылар векторының барлық құрастырушылары қатысса, онда жүйе бақыланатын деп аталынады. Егер
күй айнымалылар векторының барлық құрастырушылары қатысса, онда жүйе бақыланатын деп аталынады. Егер 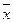 векторының бірде бір құраушысы жүйенің шығысының
векторының бірде бір құраушысы жүйенің шығысының  пайда болуына әсер етпесе, онда мұндай жүйелер бақыланбайтын болады.
пайда болуына әсер етпесе, онда мұндай жүйелер бақыланбайтын болады.
Жүйенің басқарылынатынын және бақыланатындығын талдау сәйкес басқарылыну және бақылану матрицаларын қолданып немесе басқарылыну және бақылану грамианаларын жүргізеді. Жоғарыда анықталған 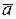 ,
, 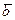 ,
, 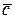 жуйенің параметрлерінің матрицаларын қолданып мына екі қосалқы матрицаларды құрастырайық
жуйенің параметрлерінің матрицаларын қолданып мына екі қосалқы матрицаларды құрастырайық
R = [ 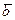 ,
, 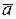
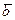 ,...,
,..., 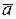 n-1
n-1 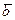 ], D = [
], D = [  ,
, 
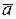 ,…,
,…, 
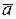 n-1].
n-1].
R және D матрицалар сәйкесінше басқарылыну және бақылану матрицалары деп аталады. MATLAB программасында осы матрицаларды ctrb және obsv командалармен құрастыруға болады.
Жоғарыда (2.17) және (2.18) теңдеулермен сипатталған АБЖ басқарылатын болу үшін басқарылыну матрицасының рангы керекті және жеткілікті тұрде толық болып n-ге тең болуы rankR = n керек.
Ал АБЖ бақыланатын болу үшін бақылану матрицанын рангы керекті және жеткілікті түрде толық болып n-ге тең болуы rankD = n керек.
Тек бір ғана кірісі мен шығысы бар АБЖ басқарылыну және бақылану матрицалар шаршы болады, сондықтан, басқарылу және бақылануды тексеру үшін R және D матрицаларының анықтауыштарын табу жеткілікті. Егер олар 0 – ге тең болса, онда матрицаның толық рангы болады.
Дата добавления: 2015-08-20; просмотров: 169 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Күй айнымалылары арқылы жүйені сипаттау. Басқарылыну және бақылау. | | | Лаплас түрлендіруі, беріліс функциясы. |