
Читайте также:
|
Лаплас түрлендіруінің кейбір маңызды түрлері.
2.1 – кесте
ƒ 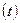
|  F F 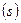
|
Қадамдық функция, u 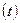
| 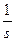
|
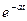
| 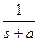
|
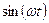
| 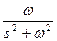
|
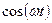
| 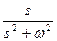
|
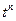
| 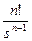
|
ƒ 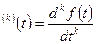
| 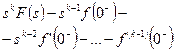
|
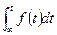
| 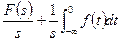
|
Импульстік функция, 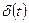
| |
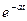 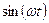
| 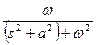
|
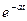 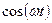
| 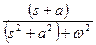
|
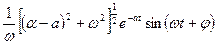 , , 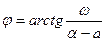
| 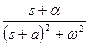
|
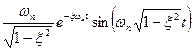 , , 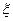 <1 <1
| 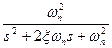
|
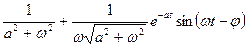 , , 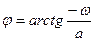
| 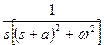
|
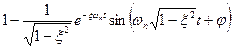 , , 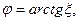 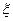 <1 <1
| 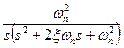
|
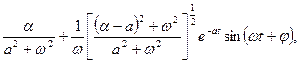 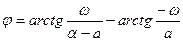
| 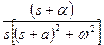
|
Жоғарыда көрсеткендей АБЖ буындарының құрастырушыларының табиғаты әр түрлі болсада (2.1)-ге ұқсас дифференциалды теңдеулермен сипатталынуы мүмкін. Осы әдiстерді әдетте жүйенің сыртқы сипаттамаларына жатқызады. Керісінше, ішкi сипаттама күй айнымалылары арқылы берiледi, олар көбінесе бірнеше кіріс және шығысы бар жүйелер үшін қолдануға ынғайлы. Айталық жүйе күйінің айнымалысы 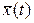 ретінде бірінші ретті туындысы АБЖ математикалық моделіне кіретін айнымалылар жиынын алайық. Басқаша айтқанда, күй айнымалысы ретінде кіріс әсермен
ретінде бірінші ретті туындысы АБЖ математикалық моделіне кіретін айнымалылар жиынын алайық. Басқаша айтқанда, күй айнымалысы ретінде кіріс әсермен 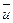 (t) қатар шығыс айнымалысы
(t) қатар шығыс айнымалысы 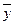 (t) және жүйенің болашақ күйін анықтауға мүмкіндік беретін айнымалылар жиынтығын айтуға болады. Күй айнымалысы арқылы белгіленген жүйенің математикалық моделі компьютерлік талдауға ыңғайлы болып келеді.
(t) және жүйенің болашақ күйін анықтауға мүмкіндік беретін айнымалылар жиынтығын айтуға болады. Күй айнымалысы арқылы белгіленген жүйенің математикалық моделі компьютерлік талдауға ыңғайлы болып келеді.
Айталық, сызықты жүйе n - күй айнымалысынан құралған 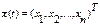 күй векторымен сипатталсын. Жүйенің кірісіне кіріс басқарушы сигналдар
күй векторымен сипатталсын. Жүйенің кірісіне кіріс басқарушы сигналдар 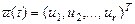 түседі. Онда жүйе төменде берілген векторлық түрдегі келесі күй теңдеуімен сипатталады:
түседі. Онда жүйе төменде берілген векторлық түрдегі келесі күй теңдеуімен сипатталады:
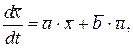 (2.17)
(2.17)
мұндағы 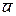 және
және  - тұрақты коэффициенттерден құрылған матрицалар, олар мына түрде болады:
- тұрақты коэффициенттерден құрылған матрицалар, олар мына түрде болады:
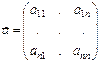 ,
, 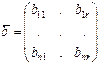 .
.
(2.17) теңдігінен басқа қарастылған жүйе үшін келесі матрицалық теңдікті жазуға болады
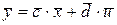 (2.18)
(2.18)
мұндағы 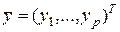 - шығыс шамалар векторы. Тұрақты шама матрицалары мына түрде болады
- шығыс шамалар векторы. Тұрақты шама матрицалары мына түрде болады
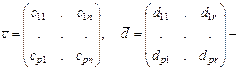
Екі (2.17) және (2.18) векторлық теңдеулер бір уақытқа t = t0 шешім тауып кез келген t>t0 уақыт үшін 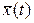 табуға, яғни жүйенің болашақ күйін болжауға, мүмкiндiк бередi, сонымен қатар, осы екі векторлық теңдеу арқылы шығыс шамалар векторы
табуға, яғни жүйенің болашақ күйін болжауға, мүмкiндiк бередi, сонымен қатар, осы екі векторлық теңдеу арқылы шығыс шамалар векторы  (t) анықталады.
(t) анықталады.
(2.17) және (2.18) векторлық теңдеулер жүйелерiнен 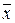 векторын шығарып тастауға болады. Бұның нәтижесіндегі теңдеу «кiрiс-шығыс» түрленуі (2.1) түріндегі тұрақты коэффициенті n-ретті сызықты дифференциалдық теңдеу болып шығады.
векторын шығарып тастауға болады. Бұның нәтижесіндегі теңдеу «кiрiс-шығыс» түрленуі (2.1) түріндегі тұрақты коэффициенті n-ретті сызықты дифференциалдық теңдеу болып шығады.
Бұдан бері қарастырылған АБЖ сиппатаулары бір-бірімен өз ара тығыз байланыста болғандықтан бір сипаттаудан басқаларын жеңіл табуға болады. Мысалы, АБЖ күйі айнымалылар арқылы сипатталған болса, онда АБЖ кешенді беріліс функциясын W(s) мына теңдеумен табуға болады
W(s)= 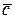 (sE-
(sE- 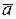 )-1
)-1 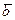 ,
,
мұндағы s – Лаплас операторы, ал Е – бірлік матрицасы.
Дата добавления: 2015-08-20; просмотров: 158 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| День - 10 день | | | Басқарылыну және бақылану |