Тема. Розв’язування задач на застосування формули Бернуллі, локальної та інтегральної теорем Лапласа.

Практичне заняття

1. Застосування формули Бернуллі.

2. Застосування локальної та інтегральної теорем Лапласа.

Задача 1. На сотню металевих брусків припадає 30 із зазубринами. Яка ймовірність, що для випадково взятих 7 брусків без дефектів буде не більше двох?

Розв’язання. Якщо подія А відповідає бруску без дефекта, то
Р(А)= Тоді n =7, k ≤2, тобто шукана ймовірність

,

застосовуючи формулу Бернуллі

Задача 2. У середньому брак виробництва складає 7,5 %. Виз­начити найвірогідніше число стандартних виробів у партії із 39 штук.

Розв’язання. Якщо q =0,075, то р =0,925 є ймовірність випуску стан­дартної деталі: n =39. На підставі подвійної нерівності маємо

39∙0,925–0,075 ≤ k ₀ ≤ 39∙0,925+0,925 маємо 36= k ₀ або k ₀=37.

Задача 3. При скількох пострілах найвірогідніше число попадань рівне 16, якщо ймовірність попадання в окремому пострі­лі 0,7?

Розв’язання. Отже, k ₀=16; р =0,7 і q =0,3. Складаємо подвійну нерівність 0,7 n– 0,3 ≤ 16 ≤ 0,7 n +0,7. Звідки і . Число всіх пострілів може бути 22 або 23.

Задача 4. Ймовірність попадання в мішень 0,7. Яка ймовір­ність того, що із 20 пострілів 15 будуть вдалими?

Розв’язання. n =20, k =15, p =0,7, q =0,3. Щоб скористатися формулою локальної теореми Лапласа , послідовно обчислю­ємо:

а) ; б) ;

в) по таблиці ; г) .

Задача 5. При транспортуванні ймовірність пошкодити виріб дорівнює 0,0005. Обчислити ймовірність, що при цьому із усіх виробів числом 4000 тільки від 3 до 5 будуть пошкодженими.

Розв’язання. n =4000, р =0,0005; λ = np ≡2. Скористаємося формулою

.

Задача 6. Частка виробів вищого сорту для продукції заводу складає 60 %. Яка ймовірність, що із 1000 шт. число згадуваних виро­бів знаходиться в межах від 580 до 630?

Розв’язання. За умовою задачі маємо: n =1000; р =0,6; q =0,4; а =580; в =630.

; ;

; ;

;

Задача 7. Ймовірність появи виробу 1-го сорту серед продук­ції – 0,7. Відхилення згадуваних виробів від найвірогіднішого їх числа серед 400 шт. За абсолютною величиною дорівнює 25. Обчис­лити ймовірність такого відхилення.

Розв’язання. За умовою задачі маємо: n =400; ε =25; р =0,7; q =0,3. Тоді =np=280; ; ; ; подвійна нерівність записується 255 ≤ k ₀ ≤ 305.

Задача 8. Ймовірність появи події А в окремому випробу­ванні – р =0,6. Знайти ймовірність того, що для 150 випрбувань частота настання такої подїї буде різниться від її ймовірності не більше, ніж на 0,03.

Розв’язання. n =150, р =0,6, q =0,4, ε =0,03. Треба шукати ймовірність , яка дорівнює .

Задача 9. Із партії, в якій 12 стандартних і 4 нестандартні деталі, навмання беруться 3 деталі з поверненням. Знайти ймовірність того, що серед узятих деталей:

1) усі три стандартні;

2) не більш як одна нестандартна;

3) принаймні одна нестандартна.

Розв’язання. Маємо схему трьох незалежних випробувань. Нехай подія А — «узята щоразу деталь стандартна», тоді 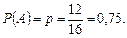Імовірності обчислюватимемо за формулою Бернуллі:

1)

2) Подію «із трьох деталей не більш як одна нестандартна» можна розглядати так: узято 3 стандартні деталі або 2 стандартні і одну нестандартну деталь. У позначеннях формули Бернуллі

3) Протилежною для даної буде подія «усі три деталі стандартні». Їй рівносильна подія Обчислимо цю ймовірність:

Задача 10. Частка довгих волокон у партії бавовни становить у середньому 0,6 загальної кількості волокон. Скільки потрібно взяти волокон, щоб найімовірніше число довгих волокон серед них дорівнювало 40?

Розв’язання. Скористаємося формулою, за якою визначається найімовірніше число: Підставимо сюди значення відомих величин:

Задача має два розв’язки: n = 66 i n = 67.

Задача 11. На кожні 40 відштампованих виробів у середньому припадає 4 дефектних. Із усієї продукції навмання узято 400 виробів. Знайти ймовірність того, що серед них 350 виробів будуть без дефектів.

Розв’язання. Подія А — «узято виріб без дефекту». За умовою Р (А) = р = 0,9. Проведено n = 400 незалежних випробувань. Розв’яжемо задачу за формулою локальної теореми

Лапласа: Підставляючи дані за умовою задачі, дістаємо:

За таблицями знаходимо беручи до уваги, що — парна функція.

Отже,

Задача 12. Завод відправив на базу 1000 доброякісних виробів. За час перебування в дорозі кожний виріб може бути пошкоджено з імовірністю 0,003. Знайти ймовірність того, що на базу прибудуть 3 пошкоджені вироби.

Розв’язання. Якщо подія А — «виріб пошкоджено», то її ймовірність р = 0,003. Розглядається схема незалежних випробувань, n = 1000. Імовірність події А досить мала, тому задачу розв’я­жемо за формулою Пуассона:

Виконуючи обчислення, знаходимо:

Задача 13. Зерна пшениці проростають з імовірністю 0,95. Знайти ймовірність того, що із 2000 посіяних зерен зійде від 1880 до 1920.

Розв’язання. Подія А — «зерно пшениці зійшло». Її імовірність р = 0,95, кількість незалежних випробувань n = 2000. Застосуємо формулу інтегральної теореми Лапласа:

функція Лапласа, а далі виконаємо обчислення:

Значення функції Лапласа беруться з відповідної таблиці.

Задача 14. Митний пост дає статистичну оцінку того, що 20% усіх осіб, що повертаються з-за кордону, не декларує весь товар, на який накладається податок. Якщо випадково відібрати 5 осіб, то яка ймовірність того, що 3 з них не задекларували весь товар?

Розв’язання. Позначимо через А подію, що навмання вибрана особа не задекларувала весь товар, Р(А) = 0,2. Задача задовольняє умовам формули Бернуллі: п = 5, к = 3,р = 0,2:

.

Задача 15. Прилад складено з 10 блоків, надійність кожного з них 0.8. Блоки можуть виходити з ладу незалежно один від одного. Знайти імовірність того, що:

а) відмовлять два блоки;

б) відмовить хоча б один блок;

в) відмовлять не менше двох блоків.

Розв’язання. Позначимо за подію А відмову блока. Тоді ймовірність події А за умовою прикладу буде Р(А) = р = 1 – 0,8 = 0,2, тому q = 1 – р = 1 – 0,2 = 0,8. Згідно з умовою задачі n = 10. Використовуючи формулу Бернуллі та Зауваження 1, одержимо:

а) Р₁₀(2) = (0.2)²(0.8)⁸ = 0.202,

б) Р₁₀(1 < m 10) = 1 – Р₁₀(0) = 1 - (0.2)⁰(0.8)¹⁰ = 0.8926,

в) Р₁₀(2 10) = 1 – (Р₁₀(0) + Р₁₀(1)) = 1 – ( (0,2) × (0,8))¹⁰ + + ) = 0,6244.

Задача 16. У разі додержання певної технології 90% усієї продукції, виготовленої заводом, є найвищого сорту. Знайти найімовірніше число виробів найвищого сорту в партії з 200 штук.

Розв’язання. За умовою задачі п = 200; р = 0,9; q = 1 – р = 0,1.

Використовуючи зауваження 2, дістаємо:

Отже, найімовірніше число виробів першого сорту серед 200 дорівнює 180.

Задача 17. Робітник обслуговує шість верстатів-автоматів. Імовірність того, що протягом години верстат-автомат потребує уваги робітника, є величиною сталою і дорівнює 0,6. Яка ймовірність того, що за годину уваги робітника потребують: 1) три верстати; 2) від двох до п’яти верстатів;
3) принаймні один.

Розв’язання. За умовою задачі маємо: p = 0,6; q = 0,4; n = 6; m = 3; ; .

Згідно з (29), (30), (33), дістаємо:

1) ;

2)

=15 (0,6)² (0,4)⁴ + 20 (0,6)³ (0,4)³ + 15 (0,6)⁴ (0,4)²+ 6 (0,6)⁵ 0,4 =
= 15 × 0,36 × 0,0256 + 20 × 0,216 × 0,064 + 15 × 0,1296 × 0,16 + 6 × 0,07776 × 0,4 =
= 0,13824 + 0,27648 + 0,31104 + 0,186624 = 0,902384;

3) = .

Задача 18. У разі додержання певної технології 90% усієї продукції, виготовленої заводом, є найвищого сорту. Знайти найімовірніше число виробів найвищого сорту в партії з 200 штук.

Розв’язання. За умовою задачі n = 200; р = 0,9; q = 1 – р = 0,1.

Використовуючи подвійну нерівність (34), дістаємо:

.

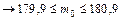Отже, найімовірніше число виробів першого сорту серед 200 дорівнює 180.

Задача 19. Імовірність того, що студент складе іспит з математики, є величиною сталою і дорівнює в середньому 0,8. Нехай є група з восьми студентів. Знайти найімовірнішу кількість членів цієї групи котрі складуть іспит з математики, і обчислити відповідну ймовірність.

Розв’язання. За умовою задачі n = 8; p = 0,8; q = 0,8.

Отже, ; .

Доходимо висновку: найімовірніша кількість студентів, які складуть екзамен, m ₀ = 7. Відповідна ймовірність дорівнює 0,524288.

Задача 20. Фабрика випускає 75% виробів 1-го сорту. Із партії готових виробів навмання беруть 400 деталей. Обчислити ймовірності таких випадкових подій:

1) виробів 1-го сорту виявиться 290 шт.;

2) 300 шт.;

3) 320 шт.

Розв’язання. За умовою задачі маємо:

n = 400; p = 0,75; q = 0,25; m = 290; 300; 320.

1) ; ;

;

;

2) ;

;

3) ;

.

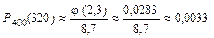Задача 21. Імовірність того, що посіяне зерно ячменю проросте в лабораторних умовах, у середньому дорівнює 0,9. Було посіяно 700 зернин ячменю в лабораторних умовах. Визначити найімовірніше число зернин, що проростуть із цієї кількості зернин, та обчислити ймовірність цього числа.

Розв’язання. За умовою задачі:

Отже, шукане число m ₀ = 630.

Відповідна ймовірність буде така:

;

;

;

.

Задача 22. Верстат-автомат виготовляє однотипні деталі. Імовірність того, що виготовлена одна деталь виявиться стандартною, є величиною сталою і дорівнює 0,95. За зміну верстатом було виготовлено 800 деталей. Яка ймовірність того, що стандартних деталей серед них буде: 1) від 720 до 780 шт.; 2) від 740 до 790 шт.?

Розв’язання. За умовою задачі:

; ; ; ; ;

.

1) ;

;

2) ;

;

Задача 23. В електромережу ввімкнено незалежно одну від одної 500 електролампочок, які освітлюють у вечірній час виробничий цех заводу. Імовірність того, що електролампочка в електромережі не перегорить, є величиною сталою і дорівнює 0,8. Яка ймовірність того, що з 500 електролампочок не перегорить:

1) не більш як 380 шт.;

2) не менш як 390 шт.

Розв’язання. За умовою задачі:

; ; ; ; ;

1)

;

2) ;

;

Задача 24. Радіоприлад містить 1000 мікроелементів, які працюють незалежно один від одного, причому кожний може вийти з ладу під час роботи приладу з імовірністю р = 0,002. Обчислити ймовірності таких випадкових подій: 1) під час роботи приладу з ладу вийдуть 3 мікроелементи; 2) від трьох до шести.

Розв’язання. За умовою задачі маємо n = 1000; p = 0,002; m = 3; 3 . Оскільки n велике, а р мале число, то для обчислення ймовірностей застосуємо формули (47) і (48). Для цього обчислимо значення параметра а = np = 1000 · 0,002 = 2.

1) .

2)

=

Задача 25. Імовірність того, що під час епідемії грипу мешканець міста захворіє на цю хворобу, становить у середньому 0,03%. Яка ймовірність того, що серед навмання вибраних 300 мешканців міста хворих на грип виявиться: 1) 5 осіб; 2) не більш як 3 особи.

Розв’язання. За умовою: p = 0,003; n = 300; m = 5;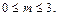

Обчислюємо значення параметра а = np = 300 × 0,003 = 0,9.

1) P ₈₀₀ (5) 0,002001.

2)

Дата добавления: 2015-08-17