Примеры. · — однородное дифференциальное уравнение второго порядка с постоянными

· — однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением является семейство функций , где и — произвольные константы, которые для конкретного решения определяются из задаваемых отдельно начальных условий. Это уравнение, в частности, описывает движение гармонического осциллятора с циклической частотой 3.

· Второй закон Ньютона можно записать в форме дифференциального уравнения 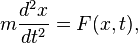где m — масса тела, x — его координата, F (x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

· Дифференциальное уравнение Бесселя — обыкновенное линейное однородное уравнение второго порядка с переменными коэффициентами: 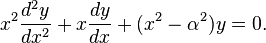Его решениями являются функции Бесселя.

· Пример неоднородного нелинейного обыкновенного дифференциального уравнения 1-го порядка:

В следующей группе примеров неизвестная функция u зависит от двух переменных x и t или x и y.

· Однородное линейное дифференциальное уравнение в частных производных первого порядка:

· Одномерное волновое уравнение — однородное линейное уравнение в частных производных гиперболического типа второго порядка с постоянными коэффициентами, описывает колебание струны, если — отклонение струны в точке с координатой x в момент времени t, а параметр a задаёт свойства струны:

· Уравнение Лапласа в двумерном пространстве — однородное линейное дифференциальное уравнение в частных производных второго порядка эллиптического типа с постоянными коэффициентами, возникающее во многих физических задачах механики, теплопроводности, электростатики, гидравлики:

· Уравнение Кортевега — де Фриза, нелинейное дифференциальное уравнение в частных производных третьего порядка, описывающее стационарные нелинейные волны, в том числе солитоны:

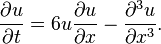
Дата добавления: 2015-08-20