Найти и упростить аналитическое выражение для общей риск-оценки жизнестойкости атакуемой КИИ, состоящей из множества исследуемых элементов.

После всех расчётов, которые были проведены в предыдущих пунктах, перейдём к нахождению общей риск – оценки эффективности атакуемой системы, состоящей их множества исследуемых компонентов. Причем при оценке всей системы в целом, будем исходить из того, что отказ одного компонента не ведет за собой отказ другого компонента. Это дает нам то, что ущербы, возникающие при отказах компонентов слабо коррелированы между собой. Отсюда следует, что общий ущерб РИС можно найти, как сумму ущербов каждой компоненты системы, но свойство независимости компонент требует, рассматривать плотность вероятностей отказа компоненты, как произведение плотностей вероятностей отказа отдельных компонент.

На распределенную систему в целом происходят два воздействия: синхронное и асинхронное.

Синхронное воздействие – это совместное воздействие дестабилизирующих факторов.

Асинхронное воздействие – это несовместное воздействие дестабилизирующих факторов.

При реализации синхронного воздействия получим следующую формулу:

где зависимость ущерба от времени ой компоненты;

- плотность вероятности отказа - ой компоненты, - количество компонент распределенной системы.

При асинхронном воздействии формула для риска будет иметь вид:

Тогда для распределения Хи-квадрат получим:

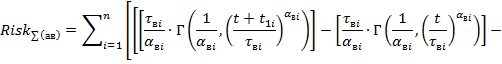
где и - постоянные времени «восхода» и «заката» жизненного цикла ой компоненты системы; - коэффициенты нелинейности ой компоненты системы, - текущее время.

Используя метод усредненных оценок, выше полученные уравнения можно упростить, используя математическое ожидание функции ущерба ( ой компоненты.

Найти аналитическую зависимость живучести без учета ущерба и с учетом ущерба. Сравнить полученные зависимости и сделать соответствующие вывод о преимуществах и недостатках того или иного расчета. Выявить какой из полученных результатов является более детальным, и какой лучше использовать.

Найдем сначала аналитическую зависимость живучести компонента системы, исключая ущерб, который этот компонент может нанести системе в результате отказа. Тогда функция живучести примет следующий вид:

где , , a 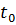– момент времени в котором считается живучесть компонента КИИ. Подставим эти выражения в формулу живучести и получим следующее:

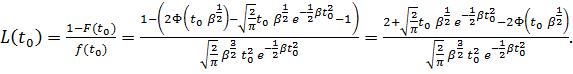(41)

Построим три графика функции живучести, при этом положим , которые отвечают функциям соответственно. В результате получим следующий график:

Рис. 12. Графики функции живучести.

Таким образом, видно, что чем больше коэффициент тем сильнее график приближается к началу координат. Если схематично изобразить это на рисунке то получим следующее:

Рис. 13. График функции живучести.

Теперь перейдем к отысканию аналитической зависимости живучести компонента системы с учетом ущерба. Формула живучести в данном случае будет выглядеть следующим образом:

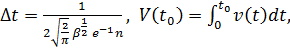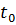где a , при этом – количество дискрет, - момент времени отказа компонента КИИ, а - момент времени в котором компонент КИИ полностью восстановился, при это .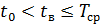

Рассмотрим случай, когда компонент КИИ безвозвратно вышел из строя и, следовательно, не подлежит восстановлению, тогда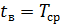

Формула живучести в этом случае будет задаваться следующим образом:

. (43)

Перейдём к расчету аналитической зависимости функции живучести. Для этого сначала посчитаем и а затем подставим их в формулу живучести:

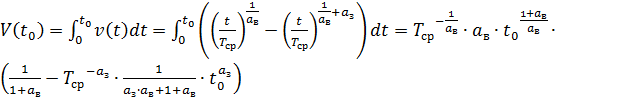, (44)

= . (45)

Следовательно, формула живучести будет выглядеть следующим образом:

. (46)

Построим три графика функции живучести, при этом положим , которые отвечают функциям соответственно. В результате получим следующую таблицу:

Построим по данной таблице графики функции живучести. Они будут выглядеть следующим образом (Рис. 14.):

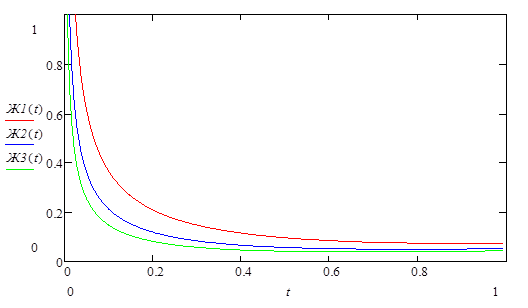
Рис. 14. Графики функции живучести.

Сопоставим график живучести без учета ущерба, с графиком живучести с учетом ущерба (Рис. 15.)

Рис. 15. Сравнение графиков живучести.

Из данного рисунка видно, что графики живучести компоненты КИИ с учетом ущерба и без учета ущерба практически полностью совпадают. Не трудно заметить, что на все области определения данные графики монотонно убывают, и ведут себя практически одинаково.

Однако в риск-анализе целесообразно использовать вторую зависимость, так как в ней использует числовая характеристика как ущерб, которая является неотъемлемой составляющей риск-анализа и дает более полную и точную оценку.

Предложить методику противодействия угрозам для рассматриваемых элементов и разработать алгоритм управления жизнестойкостью многокомпонентной КИИ, а также - осуществить вычислительный эксперимент по риск-оценке и регулированию жизнестойкости КИИ, состоящей из нескольких элементов исследуемой разновидности.

Дата добавления: 2015-08-18