Обоснование типа, класса и вида КИИ

В качестве исследуемого компонента выберем тип системы управления «файловый сервер», используя статистические данные об отказе отдельной части данной системы.

По данным сайта Arbor Networks после 11 дней наблюдения (с 2008-01-03 по 2008-01-14) система стала неспособной выполнять свои функции. Но после реализации угрозы система была восстановлена. Ниже представлены статистические данные (таблица 1) и полученная на их основе гистограмма (рис. 4).

Функция полезности:

, (1)

где α_в и α_з – коэффициенты нелинейности (восхода и заката соответственно);

τ_в и τ_з – постоянные времени «восхода» и «заката» жизненного цикла компонента; t – текущее время;

Проверка соответствия эмпирического распределения атак на файловый сервер теоретическому.

В следующей таблице представлены результаты подсчёта количества атак в день на компонент системы в течение 11 дней.

Таблица 1 – Статистические данные атаки

День
Число атак

Требуется проверить гипотезу о согласии данной выборки со стандартным распределением Хи-квадрат.

Плотность вероятностей распределения Хи-квадрат имеет вид:

Для проверки гипотезы воспользуемся критерием согласия Пирсона.

Используем формулу статистики:

где 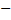предполагаемая вероятность попадания в -й интервал;

- соответствующее эмпирическое значение;

- число элементов выборки из каждого интервала;

N – объем выборки.

При заданном распределении атак, и объеме выборки N=558 атак, получаем следующие вероятности (таблица 2).

Таблица 2 – Частотные вероятности

	0,30706		0,00013455
	0,33602		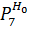0,0000132
	0,14303		0,0000031
	0,02143		0,00000268
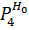
	0,00815		0,000000612
	0,001223

Подставляя в формулу для оценки статистики, получаем: = 13,621.

Для заданного уровня значимости α=0.1 и заданными 9 степенями свободы, имеем: =15,135.

Следовательно, гипотеза о том что, статистика имеет распределение Хи-квадрат, не отвергается на уровне значимости α=0.1 так как: <

Для наглядности построим график плотности вероятности при заданных коэффициентах = 1, = 2, = 3, = 4, = 5 (рис. 3).

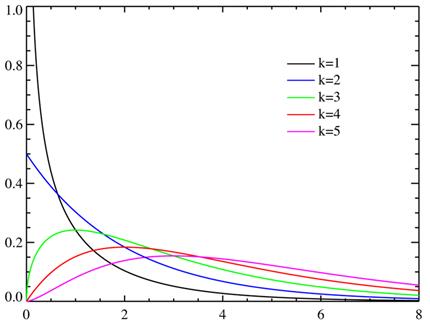
Рисунок 3 – Плотность распределения вероятности

Рисунок 4 – Гистограмма распределения статистики атак

Дата добавления: 2015-08-18