Найти и исследовать аналитическую зависимость (от времени) ущерба (как упущенной выгоды и др.) выражения полезности элемента КИИ.

Для того чтобы найти и исследовать аналитическую зависимость ущерба нужно взять интеграл от функции полезности с пределами от t₁ до t_2.

Данная функция полезности

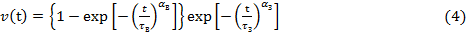
где t_в,t_з - постоянные времени «восхода» и «заката» жизненного цикла компонента; a_в , a_з - коэффициенты нелинейности > 1.

При этом производительность (полезность) функционирования элемента КИИ выражается следующими зависимостями от времени:

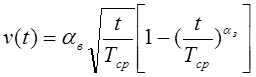, (5)

где 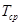– среднее время жизни системы.

Построим график функции полезности.

1)

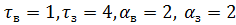
2)

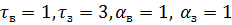
3)

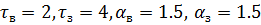
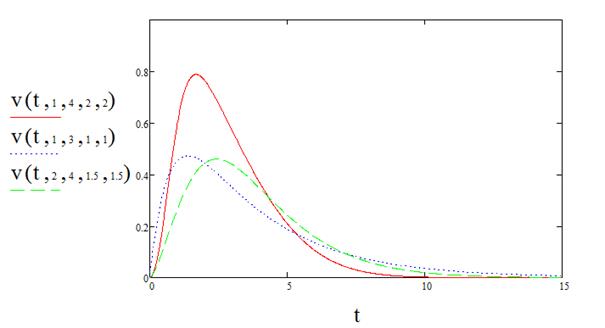
Рисунок 5 – График функции полезности

Для расчета аналитического выражения ущерба:

Интегрирование производится от начала атаки 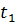до конца атаки 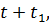так как система только временно теряет работоспособность объекта. Проще говоря 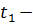это длительность ликвидации последней успешной атаки. Для начала упростим выражение полезности компоненты системы:

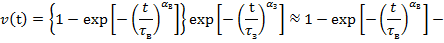
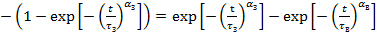, (7)

Проинтегрируем данное выражение и получим аналитическое выражение ущерба:

 

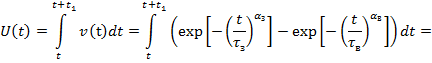
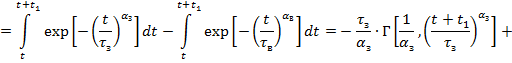
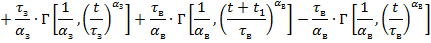
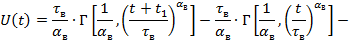
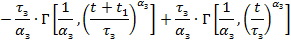
где t_в,t_з - постоянные времени «восхода» и «заката» жизненного цикла компонента; a_в , a_з - коэффициенты нелинейности > 1.

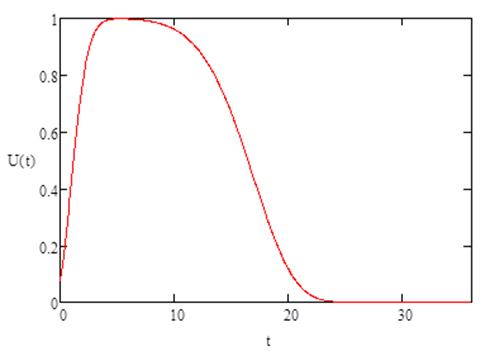
Рисунок 6 – График ущерба

3. Найти аналитическое выражение и провести его математический анализ временной зависимости риска «отказа» атакуемого элемента КИИ, включая параметры риска: пик, мода, крутизна, диапазон по уровню риска, шаг дискретизации.

Риск является одним из важнейших показателей при выборе и построении системы защиты от вероятностных угроз. По его параметрам можно определить тип защиты, разработать алгоритм управления эффективностью системы и т.д. Однако чтобы риск как можно более точно отображал ситуацию, нужно иметь большое количество данных (статистики), что не всегда возможно.

Для того, чтобы получить аналитическое выражение риска, нужно полученное выражение для ущерба умножить на плотность вероятности заданного распределения.

где 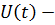зависимость ущерба от времени;

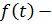плотность вероятности отказов компонентов.

 

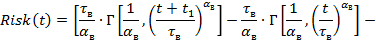
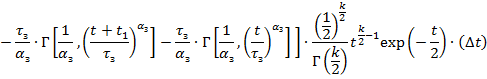
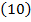
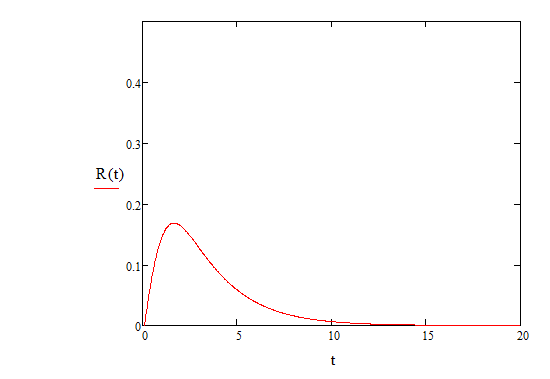
Рисунок 7 – График функции риска

Найдем параметры риска в аналитическом виде:

Найдем моду риска. Пусть 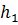– искомая мода. Тогда используя вид функций плотности вероятности отказов (f) и функции ущерба (u) мы можем записать два первых слагаемых для функции f в виде ряда Тейлора. Остальные слагаемые можно отбросить, так как они очень малы, и ими можно пренебречь.

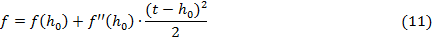
где 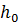- мода распределения. Для распределения Хи-квадрат она равна 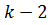_. В моей работе я заменял её на 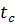, поэтому так же сделаю данную замену для вычисления моды, пика и шага дискретизации риска.

Тогда для функции ущерба мы можем аналогично записать:

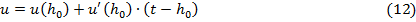
Так как 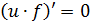, то

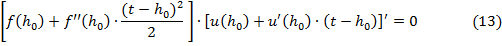
Сделаем замену: 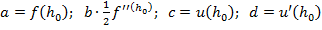, тогда

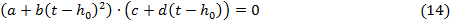
Сделаем ещё одну замену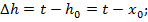

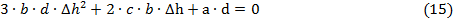
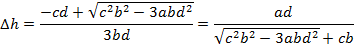
В явном виде получим:

 

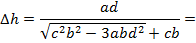
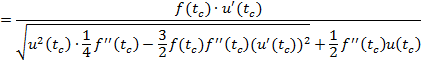
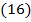
где 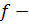плотность вероятности,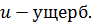

В ходе решения получится два 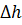. Из них будет верным тот, который будет возрастать с ростом 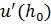. Второй 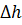просто отбрасывается.

Тогда мода риска .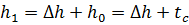

Найдем пик риска. Используя выше написанные выкладки, получим:

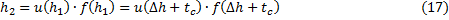
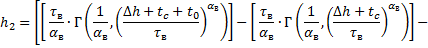
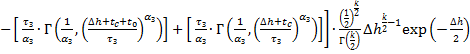, (18)

где 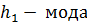риска.

Зная пик и моду можно найти крутизну: Крутизна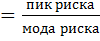

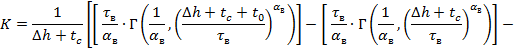
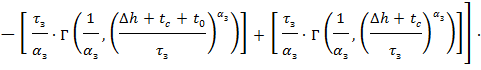
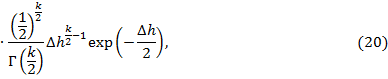
Шаг дискретизации 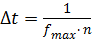, где f _max - максимальная точка плотности вероятности (удобно находить из графика); n 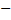количество интервалов, на которое разделим распределение.

Тогда, график риска появления негативного события в определенный момент 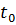имеет следующий вид (рис. 8):

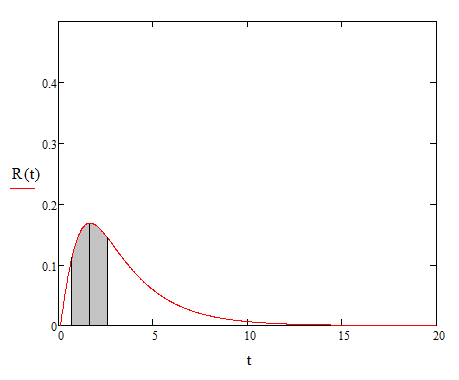
Рисунок 8 – Вероятность момента определенного во времени

Если существует вероятность появления негативного события с начала жизни системы и до определенного момента 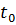формула плотности вероятности примет следующий вид:

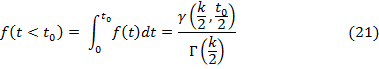
где 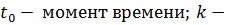параметр распределения.

Ущерб нужно усреднить

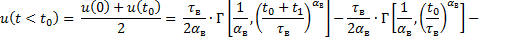
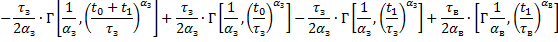
Отсюда усредненный риск будет равен

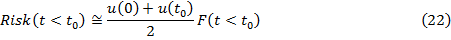
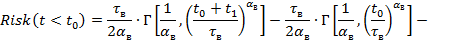
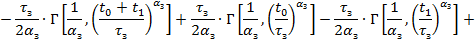
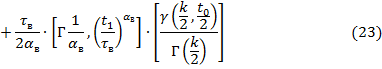
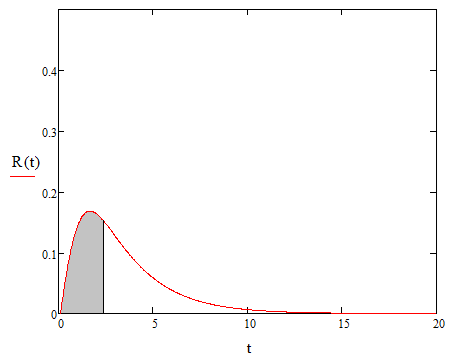
Рисунок 9 Вероятность появления негативного события с начала жизни системы и до определенного момента

В случае, когда негативное событие может проявиться в известный отрезок времени от 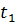и до 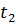, формула плотности вероятности будет иметь следующий вид:

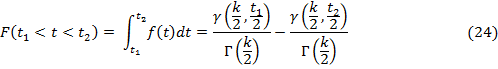
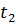и 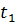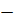границы интервала времени;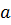 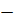параметр распределения.

Риск того, что событие произойдет в период времени 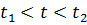, будет равен:

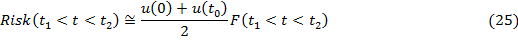
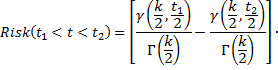
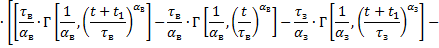
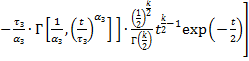(26)

График риска появления негативного события в интервале времени 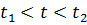имеет следующий вид (рис. 10):

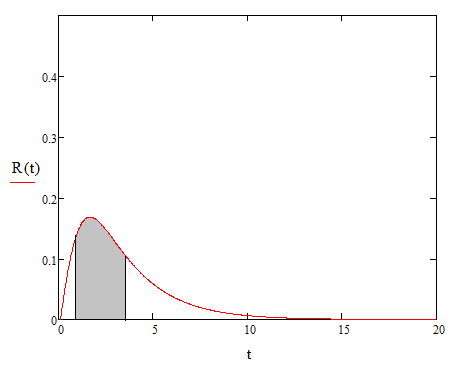
Рисунок 10 Вероятность появления негативного события в интервале времени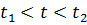

Дата добавления: 2015-08-18