
Читайте также:
|
| Найдите область определения функции y=f(x) | Найдите значения аргумента при которых функция y=f(x) положительная | Найдите значение функции у в точке x  , если , если
| Найдите
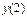 , , 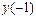 , , 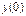 , , 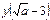 .
Постройте график данной функции.
Определите свойства функции по графику .
Постройте график данной функции.
Определите свойства функции по графику
| Найдите функцию, обратную данной. Укажите область определения и область значений обратной функции. Постройте графики данной функции и обратной в одной системе координат | |
| * | а) y= 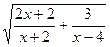 б)
б) 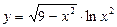
| y= 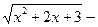 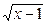
| y = 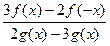 f(x)-чётная, g(x)-нечётная, f(x0)=5,g(x0)=1
f(x)-чётная, g(x)-нечётная, f(x0)=5,g(x0)=1
| 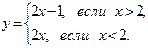
| а) 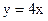 б)
б) 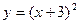 , , 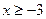 в)
в) 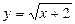
|
а) y= 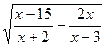 б)
б) 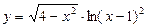
| y= 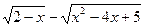
| y = 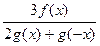 f(x)-нечётная, g(x)-чётная, f(x0)=5,g(x0)=3
f(x)-нечётная, g(x)-чётная, f(x0)=5,g(x0)=3
| 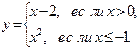
| а) 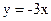 б)
б) 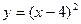 , , 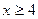 в)
в) 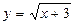
| |
а) y= 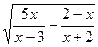 б)
б) 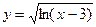
| y= 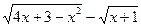
| y = 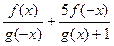 f(x)-чётная, g(x)-чётная, f(x0)=0,g(x0)=1
f(x)-чётная, g(x)-чётная, f(x0)=0,g(x0)=1
| 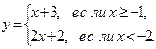
| а) 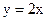 б)
б) 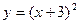 , , 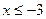 в)
в) 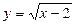
| |
а) y= 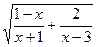 б)
б) 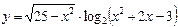
| y= 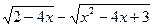
| y = 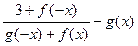 f(x)-нечётная, g(x)-нечётная,f(x0)=2,g(x0)=4 f(x)-нечётная, g(x)-нечётная,f(x0)=2,g(x0)=4
| 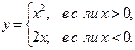
| а) 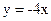 б)
б) 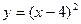 , , 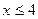 в)
в) 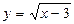
| |
а) y= 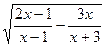 б)
б) 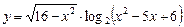
| y= 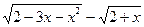
| y = 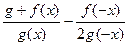 f(x)-чётная, g(x)-нечётная, f(x0)=1,g(x0)=2
f(x)-чётная, g(x)-нечётная, f(x0)=1,g(x0)=2
| 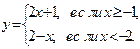
| а) 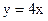 + 1
б) + 1
б) 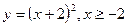 в)
в) 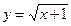
|
а) y= 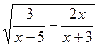 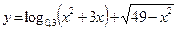
| y= 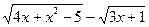
| y = 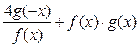 f(x)-нечётная, g(x)-чётная, f(x0)=3,g(x0)=4 f(x)-нечётная, g(x)-чётная, f(x0)=3,g(x0)=4
| 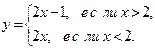
| а) 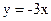 - 2
б) - 2
б) 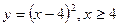 в)
в) 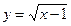
| |
а) y= 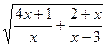 б)
б) 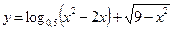
| y= 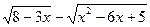
| y = 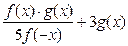 f(x)-чётная, g(x)-чётная, f(x0)=1,g(x0)=3
f(x)-чётная, g(x)-чётная, f(x0)=1,g(x0)=3
| 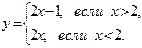
| а) 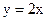 + 3
б) + 3
б) 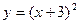 , , 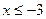 в)
в) 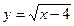
| |
а) y= 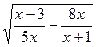 б)
б) 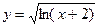
| y= 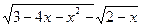
| y = 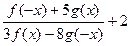 f(x)-нечётная, g(x)-нечётная,f(x0)=6,g(x0)=0 f(x)-нечётная, g(x)-нечётная,f(x0)=6,g(x0)=0
| 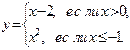
| а) 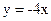 - 1
б) - 1
б) 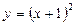 , , 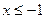 в)
в) 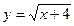
| |
а) y= 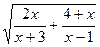 б)
б) 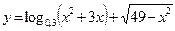
| y= 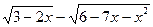
| y = 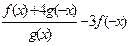 f(x)-чётная, g(x)-нечётная, f(x0)=2,g(x0)=3 f(x)-чётная, g(x)-нечётная, f(x0)=2,g(x0)=3
| 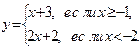
| а) 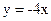 - 2
б) - 2
б) 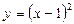 , , 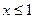 в)
в) 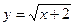
| |
а) y= 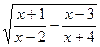 б)
б) 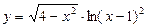
| y= 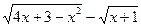
| y = 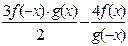 f(x)-нечётная, g(x)-чётная, f(x0)=1,g(x0)=0 f(x)-нечётная, g(x)-чётная, f(x0)=1,g(x0)=0
| 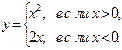
| а) 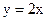 - 4
б) - 4
б) 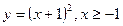 в)
в) 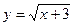
| |
а) y= 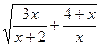 б)
б) 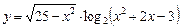
| y= 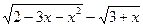
| y = 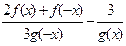 f(x)-нечётная, g(x)-нечётная,f(x0)=0,g(x0)=2 f(x)-нечётная, g(x)-нечётная,f(x0)=0,g(x0)=2
| 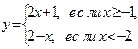
| а) 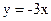 + 1
б) + 1
б) 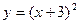 , , 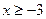 в)
в) 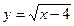
|
Дата добавления: 2015-08-17; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение тригонометрических уравнений | | | Простейшие преобразования графиков функций |